线段比的值问题(线段和值问题思路)

导语：三条思路分析一道“线段比”最值几何简题

一道简炼的几何问题往往蕴藏着丰富的知识点，认真思考也可挖掘出多条思路，对提高解题能力有一定帮助。下面是一道常见的几何题，求解“线段比”的最值，现分析编选了三条求解思路，虽然简单，但也值得思考。（供参考）

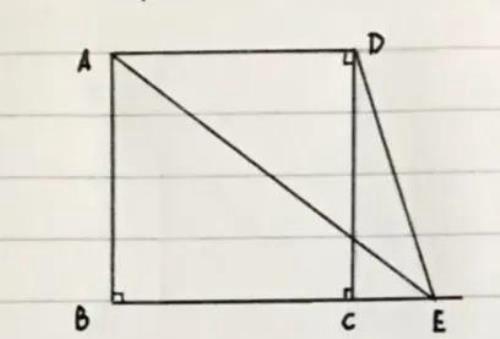
【题】（如图）正方形ABCD中，点E为射线BC上一点，连AE、DE，求：DE/AE的最小值。

思路一：造全等三角形，找“定长”折线段

过点D作DE的垂线，交AB于一点F，即DF⊥DE，则：△ADF≌△CDE，取DF中点P，连PA、PE，折线段APE的长可度…（过程见下）

思路二：数形结合，构造方程求最值

选一变量，线段CE，设CE=x，设AB=a（定值），由余弦定理得方程，利用方程根的存在意义求线段比值的大小区间…（过程见下）

思路三：利用对称变换，找定长折线段

作点D关于BC的对称点F，先造△DEF∽△AEG，将双动线段比转化为单动线段比，同时，再得△ADE≌△GFE，创造出定长折线段AFG…（过程见下）

此题型可有多种变形，即：题中正方形可变更为正三角形、等腰三角形及三角形等，而以上的三种思路具有其一般性。

本文内容由快快网络小奈整理编辑！