双动点求线段小值(双动点值问题的常用解法)

导语：“双动点”线段最值问题的转换技巧“三例说”

“线段最值”是平面几何中比较常见的一类问题，难易不一，特别当线段的两端匀为动点“双动点”时，难度会骤增，求解时必须先作适当转换，转换过程颇有技巧，现举以下三例看一看转换诀窍：

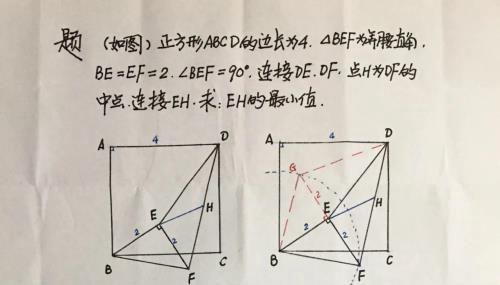
【例一】（如图）正方形ABCD的边长为4，△BEF为等腰直角，BE=EF=2，∠BEF=90º，连接DE、DF，点H为DF的中点，连接EH，求：线段EH的最小值。

【分析】首先，线段EH两端点匀为动点“双动点”线段，必须转换；然后，由H为中点的启发，造中位线（如图），EH=DG/2，此时，DG中端点D为定点；最后，只要确定点G的轨迹，求DG的最值…（过程见下）

【例二】（如图）正方形ABCD，E是AD上的一动点，以CE为边在CE的右侧作正方形CEFG，连DG、BE，若AB=4，求：BG＋BE的最小值。

【分析】首先，利用“瓜豆”确定点G的轨迹；然后，由于点E亦为动点，须转换：（BE＋BG）中BE的位置；最后，利用“饮马”求解…（过程见下）

【例三】（如图）圆O直径AB为4，C是⊙O上的一动点，将BC绕点B顺转90º至BD，连接OD，取中点M，连接CM，则CM的最小值是多少？

【分析】首先，线段CM为“双动点”线段，那么需要转换；然后，延长DC至N，使C为DN的中点，连ON（CM为中位线）；最后，由主动△OBC和从动△BCN间利用“瓜豆”求点N轨迹…（过程见下）

以上分析“三例说”，“道听度说”供参考。

本文内容由快快网络小冰整理编辑！