芝诺悖论证明(芝诺悖论错在哪里用哲学的观点解释)

导语：怎样论证芝诺悖论的二分法

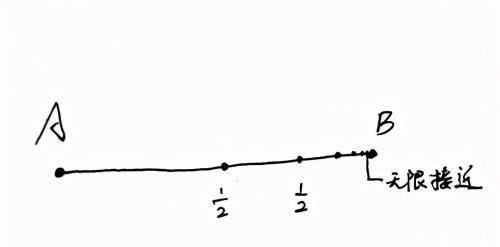
芝诺悖论的二分法：你要到某个距离的目标，必经过½的点，再剩下的½ 的½直至无穷，所以你可以无限接近但永远到不了。

这是很有意思的话题，要从A点到达B点，只要过去就好了，但是芝诺认为你永远的到不了B点。

根据此图（画的草率）一条线段如果这样分，能分成无限段，那么确实只能无限地接近B点而不能到达B点。

可是根据现实我肯定能到达B点。

根据“真”的出发却论证了“假”的到不了而实际又能到的就称之为“悖论”

悖论的论证往往是通过正确的推理形式得出的，按照逻辑学：真的前提再加上正确的推理形式得出的应该就为真。

所以我要论证的是我们确实到不了就行了，那么就不能称之为悖论了。

1，世界由原子组成，而原子间有缝隙（不讨论再细分的中子质子）我的B点在一个原子上，所以永远的到不了B点。连无限接近都做不到。

2，时间是不是连续的，假设时间是不连续的，那么在我们无限接近B点的时候，经过所剩½的时间也越短，只要时间能够继续分割，那么就能无限接近下去。

3，既然B点在终点，那我在A，B之间设置中点C点，从A到C点也只能无限接近；又在AC之间设中点D，A点也不能到达D点；以此类推，我发现我根本不能从A点出来。那都出不来了还怎么到B点呢！

各位看官，你觉得二分法这些悖论有论证的可能吗？

本文内容由快快网络小若整理编辑！