锥体的内切球体积公式(锥体内切球万能公式)

导语：立体几何中锥体的内切球问题专项练习

相比于几何体的外接球，内切球问题不是高考中的常考内容，和外接球相比，内切球问题的出题类型较少，技巧和难度也相对较低，在柱体中内切球的相关题目较为简单，因此本次内容只考虑在锥体中内切球问题。

处理锥体中内切球问题时，我们常用转化法，利用锥体的体积和面积的比值来求半径，即R=3V/S，相类比，在三角形中内切圆的半径r=2s/a+b+c，这两个公式是处理内切球问题中最常用的两个，内切球问题其实就是锥体体积和表面积问题，处理时依旧可转化为平面几何中长度的求法，由于此类问题较少，今选取8道相关的题目予以分享。

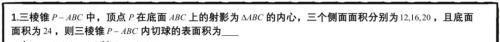
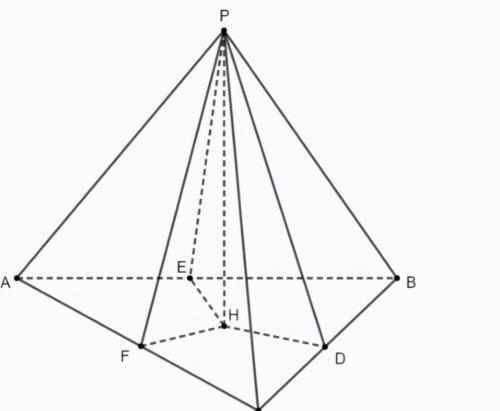
表面积已知，只需求出体积即可，加之知道底面积，只需求出三棱锥的高PH，因为H点为底面三角形的内心，因此从H点向三边作垂线，如上图所示，因为HD为底面三角形的内切圆直径，根据r=2s/a+b+c，需要求出三边边长，求出边长之后再利用条件中已知的侧面积，即可求出斜高。

上述过程是最常见的步骤，利用转化法求得内切球的半径，若类似于外接球，直接找到内切球的球心，构造三角形，利用三角形边和角的关系直接求出外接球的半径，H为内心，则内切球球心肯定在高PH上，本题目能很容易判断出三个二面角相等，只需求出侧面与底面的二面角，利用角度和底面内切圆的半径即可求出内切球的半径，这种做法有局限性，假如顶点在底面上的投影不是内心的话，这种题目就做不了了。

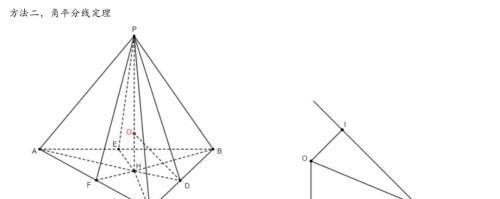
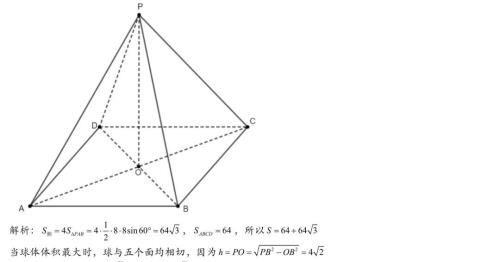
锥体的内切球问题常见于规则的锥体中，例如正三棱锥，正四面体，正四棱锥，之前给出过在正四面体中的一些常见结论，虽说直接使用结论的题目在高考中几乎不存在，但利用一些常用结论一定程度上能简化很大的计算量，与正四面体有关的常用结论如下：

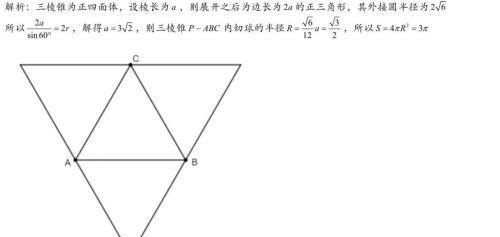
正四面体棱长和底面边长的长度不确定，但根据体积能找到边长和侧棱长的的关系，利用这种做法也能求出内切球体积的最大值，换种思路，类似于第一题的第二种做法，R与r以及侧面与底面所形成的二面角θ有关，设出底面边长a，用a和θ表示出体积，再用体积等式去掉变量a，转化为θ的函数即可求出最值。

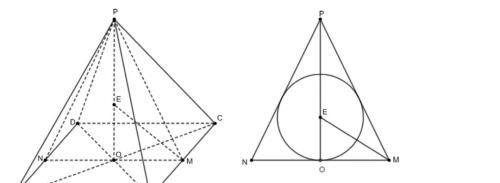
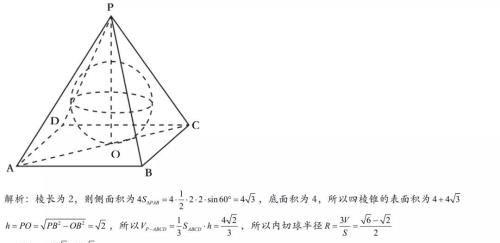
根据内切球的表面积可得到正四棱锥体积和表面积的转化关系，设出底面边长和高，利用已知的球半径和三角形相似找到a与h的转化关系，求出体积的最小值即可求出面积的最小值。

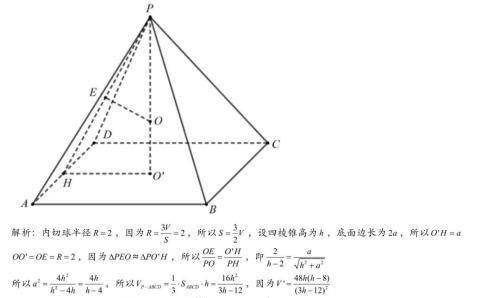
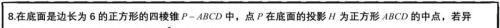
底面是正方形，且顶点在底面的投影是底面正方形的中心，则四棱锥为正四棱锥，内切球外接球的的球心均在其高线上，这是解题的关键，利用异面直线夹角求出侧高，进而求出正四棱锥的高，构造三角形即可求出外接球的半径。

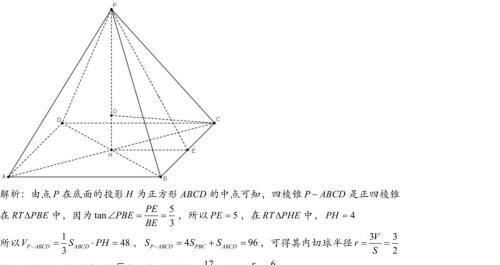
总体来说，内切球问题的解法相对单一，较难的题目例如第1题，在知道顶点在底面上的投影为底面三角形的内心后就基本上知道怎么去解了，高中阶段解内切球问题时所要求的的锥体很特殊，这就注定了在高考中不会很常见，解题用转化法变成锥体中常见数值的求法，因此在文科高考中有可能出现，以后再积累一些，积累够了再分享出来。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小茹创作整理编辑！