阿氏圆值模型(阿氏圆值问题公式)

导语：最短路径之阿氏圆（PA+k·PB型）问题探究

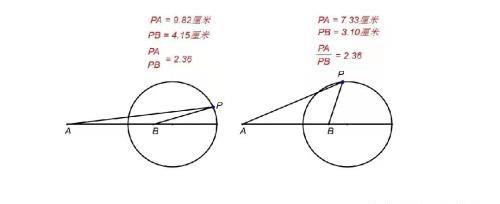
知识精讲

在平面上，到线段两端距离相等的点，在线段的垂直平分线上，即对于平面内的定点A、B，若平面内有一动点P满足PA:PB＝1，则P点轨迹为一条直线（即线段AB的垂直平分线），如果这个比例不为1，P点的轨迹又会是什么呢？两千多年前的阿波罗尼斯在其著作《平面轨迹》一书中，便已经回答了这个问题。接下来，让我们站在巨人的肩膀上，一起探究PA：PB＝k（k≠1）时P点的轨迹。

对于平面内的定点A、B，若在平面内有一动点P且P满足PA：PB＝k（k≠1），则动点P的轨迹就是一个圆，这个圆被称为阿波罗尼斯圆，简称“阿氏圆”，如图所示：

几何“PA + k·PB”型的最值问题．

如图2所示，⊙O 的半径为 r，点 A，B 都在圆外，P 为⊙O 上的动点，已知 r = k·OB，连接 PA，PB，则当“PA + k·PB”的值最小时，P 点的位置如何确定?如图3所示，在线段 OB 上截取 OC 使 OC = k·r，则可说明△BPO∽△PCO，即 k·PB = PC．因此，求“PA + k·PB”的最小值转化为求“PA + PC”的最小值，即 A，P，C 三点共线时最小(如图 4 所示)．

专题导例

1.如图，已知正方形ABCD的边长为2，以点A为圆心，1为半径作圆，E是⊙A上的任意一点，将点E绕点D按逆时针方向旋转90°得到点F，则线段AF的长的最小值　　．

方法点睛

“阿氏圆”解题一般步骤:

(1)连接动点 P 至圆心 O(将系数不为 1 的线段的两个端点分别与圆心相连接)，即连接 OP，OB;

(2)计算出所连接的这两条线段 OP，OB 的长度;

(3)计算这两条线段长度的比 =K ;

(4)在 OB 上取点 C，使得= ，即:半径的平方 = 原有的线段 × 构造线段;

(5)连接AC与圆O的交点即为点 P．

要点：如图5，构造△PAB△CAP，得到=AB·AC，

即：半径的平方=原有线段 × 构造线段

口诀：路径成最短，折线变直线

典例精讲

类型一：圆中的阿氏圆问题

例1如图，已知AC＝6，BC＝8，AB＝10，⊙C的半径为4，点D是⊙C上的动点，连接AD，连接AD、BD，则AD+BD的最小值为______ .

方法一：阿氏圆模型

对比一下这个题目的条件，P点轨迹是圆，A是定点，我们需要找出另一个定点M使得PM:PA=1:2，这就是把“阿氏圆”的条件与结论互换了一下；

而且这种问题里，给定的圆的位置、定点A的位置、线段的比例等，往往都是搭配好的！

P点轨迹圆的圆心C点和A点在直线AC上，故所求M点在AC边上，考虑到PM：PA=1:2，不妨让P点与D点重合，此时DM=DA=1，即可确定M点位置．

如果对这个结果不是很放心，不妨再取个特殊的位置检验一下，如下图，此时PM=3，PA=6，亦满足PM:PA=1:2．

方法二:构造相似三角形

注意到圆C半径为2，CA=4，连接CP，构造包含线段AP的△CPA，在CA边上取点M使得CM=2，连接PM，可得△CPA∽△CMP，故PA：PM=2:1，即PM=PA．

问题转化为PM+PB最小值，直接连BM即可．

【问题剖析】

（1）这里为什么是PA？

答：因为圆C半径为2，CA=4，比值是1:2，所以构造的是PA，也只能构造PA．

（2）如果问题设计为PA+kPB最小值，k应为多少？

答：根据圆C半径与CB之比为2:3，k应为．

类型二：与抛物线有关的阿氏圆问题

例2．如图，顶点为C的抛物线y=ax2+bx（a＞0）经过点A和x轴正半轴上的点B，连接OC，OA，AB，已知OA=OB=2，∠AOB=120°．

（1）求这条抛物线的解析式；

（2）过点C作CE⊥OB，垂足为E，点P为y轴上的动点，若以O，C，P为顶点的三角形与

△AOE相似，求点P的坐标；

（3）若将（2）的线段OE绕点O逆时针旋转得到OE′，旋转角为α（0°＜α＜120°），连接E′A，E′B，求E′A+E′B的最小值．

【分析】（1）根据AO=OB=2，∠AOB=120°，求出A点坐标，以及B点坐标，进而利用待定系数法求二次函数解析式；

（2）∠EOC=30°，由OA=2OE，OC=，推出当OP=OC或OP′=2OC时，△POC与△AOE相似；

（3）如图，取Q（，0）．连接AQ，QE′．由△OE′Q∽△OBE′，推出==,推出E′Q=BE′，推出AE′+BE′=AE′+QE′，由AE′+E′Q≥AQ，推出E′A+E′B的最小值就是线段AQ的长；

本文内容由快快网络小鸣整理编辑！