初中角平分线的定义(初中数学角平分线问题三大模型)

初中数学：角平分线的性质，搞懂了就是为中考加分

初中数学：角平分线的性质，搞懂了就是为中考加分！

角平分线的性质：

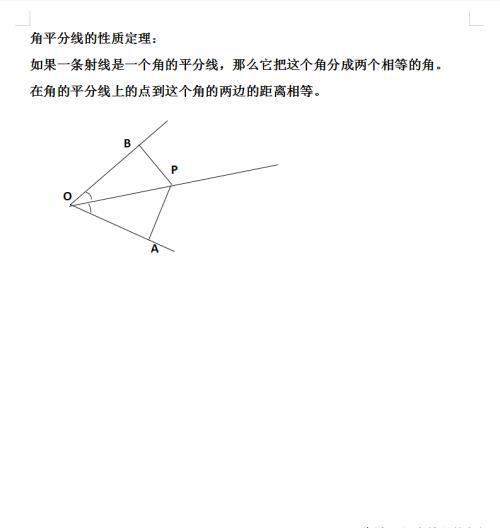
如果一条射线是一个角的平分线，那么它把这个角分成两个相等的角。

在角的平分线上的点到这个角的两边的距离相等。

如图，即PB=PA

为什么呢？

我们一起求证一下。

以OP为轴，反折，得OA=OB

在△BOP和△AOP中

OA=OB

∵∠BOP=∠AOP

OP=OP,

∴△BOP≌△AOP（SAS）

∴PB=PA

当我们做题时，当知道在角的平分线上的点到这个角的两边的距离相等时，在题中不需要证明为什么相等？这是角平分线的性质。

我们看看例题：

【例2】（1）证明：三角形的三个角的角平分线交于一点。

证明三个角交于一点，是比较难的，但两条不平行的直线是交于一点。

如图：OA是∠A的平分线，OB是∠B的平分线，它们不平行，即它们是会交于一点O。若∠C的角平分线OC也交于O点，那么三角形的三个角的角平分线就交于一点了。

实际上，已知：∠1=∠2，∠3=∠4，求证：∠5=∠6.

既然是角平分线，那么我们先用角平分线的性质来解题，看是否可以解答。

在角的平分线上的点到这个角的两边的距离相等。

所以分别做OP⊥AB,ON⊥BC,OM⊥AC，垂足分别为P,N,M点

在△APO和△AMO中

∠1=∠2

∠APO=∠AMO=90°

AO=AO

∴△APO≌△AMO（AAS）

∴OP=OM

同理△BPO≌△BNO（AAS）

∴OP=ON

∴OM=ON

在△COM和△CON中

∠CNO=∠CMO=90°

OM=ON

CO=CO

∴△COM≌△CON（HL）

∴∠5=∠6

∴三角形的三个角的角平分线交于一点

本文内容由快快网络小春整理编辑！