一半模型的面积公式(一半模型总结)

导语：最全“一半”模型结论，掌握这些面积计算不再难

一半模型是等积变换模型的延伸，但是学生往往遇到此类题目之后很难想到用等积变换的方法，所以专门提炼出一半模型，帮助学生加深此部分知识点的理解，提高面积计算的应用能力。

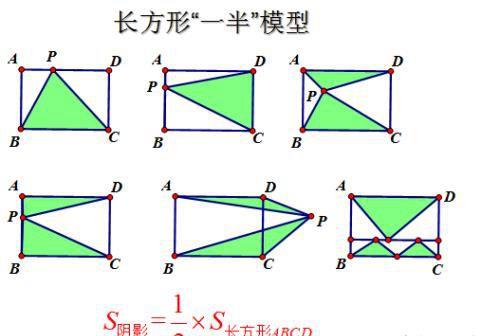
长方形“一半”模型

下图当中阴影均占长方形ABCD的一半，如果把长方形换作平行四边形，下面结论仍然成立，只是在考察当中多以长方形形式出现，如果换作平行四边形也要理解。

进一步可得如下阴影占长方形ABCD面积的四分之一：

如果把P点移动到下图位置，也就是P点在长方形两条长所在直线的外部，那可得阴影面积差（大减小）占长方形ABCD面积的一半。

三角形“一半”模型

解释一下第二行第一个图形，三角形的三条中线在三角形内部交于一点，该点称作重心，三条中线把三角形分成6个小三角形，这6个小三角形的面积是相等的，因此任取3个三角形的面积和占三角形ABC面积的一半。

四边形“一半”模型

这三个结论比较简单，不用过多解释，其中中间的四边形对边中点连线把四边形分成四块，这四块刚好可以拼成一个平行四边形。感兴趣的可以拼一下试试。

梯形“一半”模型

梯形是四边形，所以四边形具备的面积性质梯形也具备，不过梯形的一组底边平行，还具备以下性质，其中最后一个图形表示在两腰中点连线上任意取一点，所得图中阴影三角形占梯形面积的一半，该点只要在腰中点连线上，在梯形外部也成立。

特殊“一半”模型

下图当中的正方形和长方形的边是平行的。如果不平行则不成立。

本文内容由快快网络小娴整理编辑！