kmp算法面试(kmp算法难吗是什么级别)
导语:高端面试必备:KMP算法
题目描述给你两个字符串 haystack 和 needle ,请你在 haystack 字符串中找出 needle 字符串出现的第一个位置(下标从 0 开始)。
如果不存在,则返回 -1 。
问题分析字符串搜索(匹配子串)是一个很经典也具有实际应用场景的问题。
针对不同难度定位(数据范围)有不同的解法:
如果只是某道题的其中一个环节的话,我们可以直接调用语言自带的 indexOf() 方法;如果是一道简单题(数据范围 ~)的话,我们可以使用「双指针」解法;如果是一道中等题(数据范围 ~)的话,则是在考察我们 KMP 等字符串匹配算法。朴素解法枚举原串 ss 中的每个字符作为「发起点」,每次从原串的「发起点」和匹配串的「首位」开始尝试匹配:
匹配成功:返回本次匹配的原串「发起点」。
匹配失败:枚举原串的下一个「发起点」,重新尝试匹配。
代码:
class Solution { public int strStr(String ss, String pp) { int n = ss.length(), m = pp.length(); char[] s = ss.toCharArray(), p = pp.toCharArray(); // 枚举原串的「发起点」 for (int i = 0; i <= n - m; i++) { // 从原串的「发起点」和匹配串的「首位」开始,尝试匹配 int a = i, b = 0; while (b < m && s[a] == p[b]) { a++; b++; } // 如果能够完全匹配,返回原串的「发起点」下标 if (b == m) return i; } return -1; }}KMP算法一种改进的模式匹配算法,是D.E.Knuth、V.R.Pratt、J.H.Morris于1977年联合 发表,KMP算法又称克努特-莫里斯-普拉特操作。
它的改进在于:每当从某个起始位置开始一趟比较后,在匹配过程中出现失配,不回溯i,而是利用已经得到的部分匹配结果,将一种假想的位置定位“指针”在模式上 向右滑动尽可能远的一段距离到某个位置后,继续按规则进行下一次的比较
比如当我们在主串下标为3匹配子串,往后继续匹配主串,在下标是10的位置主串和 子串不匹配,这个时候就要把子串往后移动到首字母相同的位置继续匹配,但其实我们中间已经匹配了很多字符了,里面是有一些额外信息在里面的。我们利用这些额外信息就可以帮我们少枚举一些东西。
KMP算法中最难的next数组的含义。
next[i]表示的就是以i为终点的后缀和从1开始的前缀相等,且相同的部分最长,这里我们默认子串下标从1开始。比如next[i]=j就表示在子串中p[1,j]=p[i-j+1,i],这里我们用p数组暂时表示子串,这个就表示子串中下标从1到j这一段和i-j+1到i是相等的, 而且长度最长。所以下次从j+1再开始继续匹配。
next 数组的值是除当前字符外(注意不包括当前字符)的公共前后缀最长长度
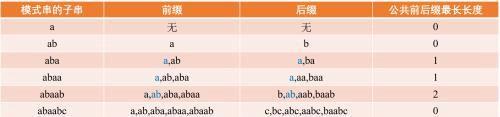
求next数组最重要的一点是找最长公共前后缀,什么是前后缀呢
前缀是除了最后一个字符的所有子串。
后缀是除了第一个字符的所有子串。
举个栗子
比如子串是ababababab,我们求他的next数组,子串下标从1开始
很明显next[1]=0,因为第一个默认是0
next[2]=0,因为没有公共前后缀
next[3]=1,最长公共前后缀是a
next[4]=2,最长公共前后缀是ab
Next[5]=3,最长公共前后缀是aba,依次类推next[6]=4.....
我们可以发现next数组的值就是子串退回时的下标
public class Solution { public static int[] getNext(String ps) { char[] p = ps.toCharArray(); int[] next = new int[p.length]; next[0] = -1; int j = 0; int k = -1; while (j < p.length - 1) { if (k == -1 || p[j] == p[k]) { next[++j] = ++k; } else { k = next[k]; } } return next; } public static int KMP(String ts, String ps) { char[] t = ts.toCharArray(); char[] p = ps.toCharArray(); int i = 0; // 主串的位置 int j = 0; // 模式串的位置 int[] next = getNext(ps); while (i < t.length && j < p.length) { if (j == -1 || t[i] == p[j]) { // 当j为-1时,要移动的是i,当然j也要归0 i++; j++; } else { // i不需要回溯了 // i = i - j + 1; j = next[j]; // j回到指定位置 } } if (j == p.length) { return i - j; } else { return -1; } }}本文内容由小思整理编辑!