导语：如何理解连续系统零极点及其对系统特性影响

什么是系统传输函数的零极点？

对于连续系统，假设系统的传输函数H(s)如下所示：

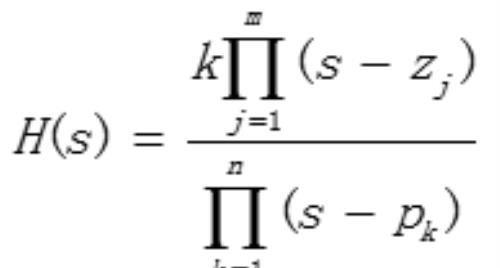
那么系统的零点为zj(系统传输函数幅值等于0的点），同理系统的极点为pk（系统传输函数幅值为无穷的点）。

例如：假设一个系统其传输函数是：

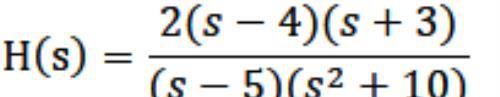
那么得到其幅度谱如下图所示（可以看到幅度谱在极点取得峰值，而在零点取得谷值）：

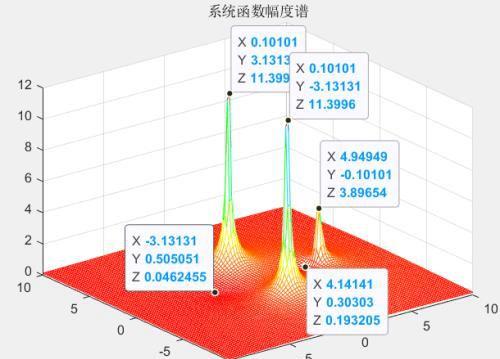
系统传输函数零极点分布对系统冲击响应的影响？

假设，一个系统其系统冲击响应h(t)分别为：e-3tu(t)，e3tu(t)，e-3tsin(3t)u(t)，cos(3t)u(t)其拉普拉斯及零极点分布分别如下图所示：

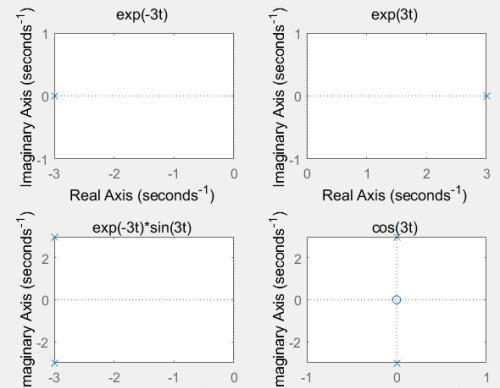
直观上可以看到：

极点如果落在S平面的左半平面，系统冲击响应呈递减趋势；

极点如果落在S平面的右半平面，系统冲击响应呈递增趋势；

系统传输函数零极点对系统频率特性的影响？

零极点对系统传输函数幅度响应的影响

从上面分析可以看出，系统极点对应系统频谱幅度的最大值，而零点对应系统频谱幅度的最低点，固假设一个系统单位传输函数的拉式变换为：

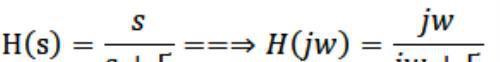
系统传输函数的幅度为：

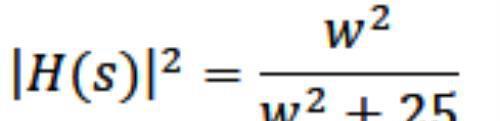
固系统传输函数的零点角频率是w0=0rad/s，此时系统传输函数的幅度|H(s)|=0；

而随着角频率w的增加系统传输函数的幅度|H(s)|趋于1，固此系统在频域表现为一个高通特性，我们可以画出该系统的频谱响应曲线如下图所示：（其结果正如我们所分析的那样呈现高通特性）

同样，当一个系统的拉式变换为：

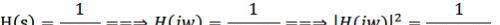
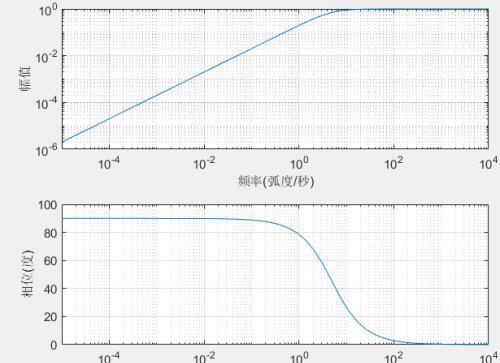
和上面的系统函数相比，该系统传输函数没有零点，但随着角频率的增加，|H(s)|变小，当w趋于无穷大时|H(s)|趋于0，故总体表现为低通特性。画出其频谱响应曲线如下所示：

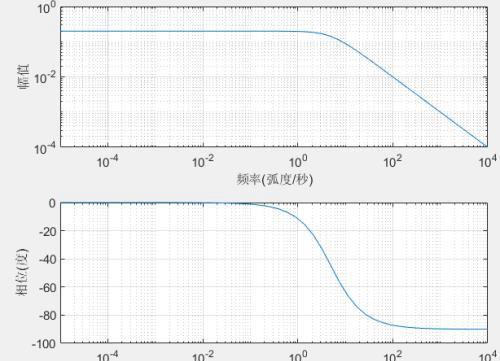
系统传输函数零极点对系统稳定性的影响？

什么是稳定系统？

所谓的稳定系统，就是当一个系统的输入是单位冲击函数数，系统的输出在t--->无穷时，系统输出y(t)趋于0，那么该系统就是稳定系统。

判断一个系统是否稳定的方法有很多种，这里以零极点分布为例进行说明。

1）、正如本节第二部分所讲，系统传输函数的极点分布对系统冲激响应的收敛有关，即如果系统的所有极点都位于s平面的左平面，那么其冲击响应在时域呈现衰减特性，相反呈现递增特性；而如果一个系统的单位冲击响应发散，那么在其他信号输入的条件下，其输出肯定发散。

这里仍然以上面的低通系统为例进行说明，假设两个系统，其一阶极点分别为-5和5，那么这两个系统的单位冲击响应分别如下图所示：

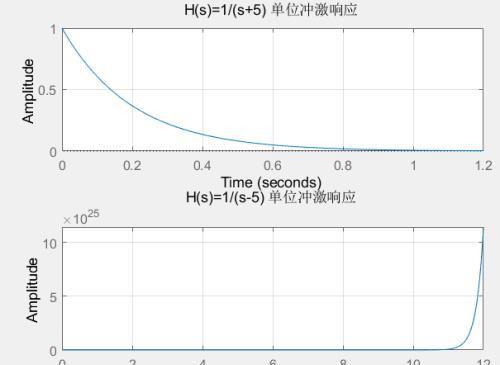
可以看到当极点5位于s平面右半平面，该系统单位冲击发散，故该系统是非稳定的。

固可以得出如下结论：

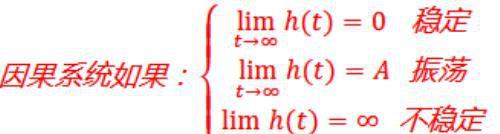
系统传输函数零极点阶数对系统频率特性的影响？

这里为了简单，以阶跃信号的拉式变换为例，进行说明，阶跃信号的拉式变换为：

则变换到对数域有：

固随着w的增加，|H(jw)|在对数域w每增加10倍，则|H(jw)|下降20dB。

当串联两个该系统，我们得到此时系统拉式变换为：

则变换到对数域有：

固随着w的增加，|H(jw)|在对数域w每增加10倍，则|H(jw)|下降40dB。

所以系统极点的阶数能够影响系统函数的幅频响应，就此例而言，系统函数如果有二阶极点，那么其对幅度的衰减是一阶极点的2倍。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小余创作整理编辑！