两正方形求阴影部分面积(如图中两个正方形中阴影部分的面积比是21)

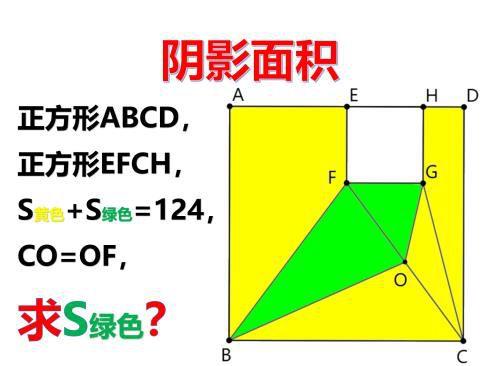
导语：求阴影面积：两正方形ABCD和EFCH，S黄+S绿=124，CO=OF，求S绿？

题目：正方形ABCD，正方形EFCH，S黄色+S绿色=124，CO=OF，求S绿色？

分析：这是一道简单的几何题目，难易程度属于初中阶段的数学题目范畴。它要求学生在正方形ABCD和正方形EFCH之间进行一些几何计算，并运用特殊的几何性质来解决问题。需要考生对正方形的特性有一定的理解和把握，并且需要掌握基本几何计算的能力，如面积计算、对应边比例关系等。因为这道题目的条件相对简单，计算过程也比较清晰明了，所以在学生的练习中广泛使用。值得注意的是，这道题目具有一定的旁证性和思维启发作用，能够培养学生的逻辑思维能力和解决问题的能力。因此对于初中学生的数学学习和知识储备的提高也有一定帮助。

解法1：∵O是CF的中点，∴S△BOC=S△BOF ，S△COG=S△FOG ，∴SBOGF=1/2S梯BCGF ，设大正方形的边长为a，小正方形的边长为b，则有 a²-b²=S黄色+S绿色=124，而S梯BCGF=½(a+b)(a-b)=(a²-b²)/2=½(S黄色+S绿色)，∴S绿色=½×S梯BCGF=½(½×(S黄色+S绿色))=¼(S黄色+S绿色) =124×¼=31。

小结：该解法完整清晰，每个步骤均有合理解释和对应的几何原理，计算过程简单明了。解法中使用了正方形的对称性原理，既简化了计算过程，又萃取了几何特性，能够帮助学生深化对几何图形的认识。该解法所使用的方法相对于其他解法来说更为直观和简便，适合初学者掌握。值得一提的是，该解法不仅注重了细节分析，还充分展现了学生的思维能力和逻辑分析能力。最后，由于难度较低，解题思路比较简单，该题目通常被用作几何图形初步训练题或课后习题，适合用来提高学生的思考能力和运算技巧。

解法2：设EFGH的边长为a，ABCD的边长为m，S梯ABFE+S梯CDHG＝½(m+a)×(m-a)，S梯BCGF＝½(m+a)(m-a)，得S梯BCGF＝½(S黄色+S绿色)＝½×124＝62，O为CF中点，S绿色＝½S梯BCGF＝½×62＝31。

小结：该解法同样简单明了，使用面积计算公式，能够有效地减少解题过程中的计算量。和解法1相比，该解法更加注重了梯形的性质，避免了正方形对称性原理的使用，突出了基础知识的运用。由于面积计算公式的简单易行，该方法适合用于几何初学者的练习，有利于学生巩固对面积计算公式的掌握。需要指出的是，虽然该解法简单明了，计算过程也比较容易，但是学生在练习时需要注意理解题意，认真把握题目所描述的几何图形特征，才能顺利地求解。总之，该解法较为基础，能够为学生提供一种较为简单的解题思路，同时也能有效地帮助学生通过几何图形的练习来提高自己的空间想象力和计算能力。

解法3：梯形FGCB面积与梯形ABFE和CDHG同底，前者高为后两者高之和，则前者面积与后两个和相等。OZ为中点，同底等高，则四边形FGOB包含的两△与四边形GOBC包含的两△面积相等。那么，S绿色＝124/2/2=31。

小结：该解法使用了四边形的性质，几何分析比较具有思维性，能帮助学生加深对几何图形的认识和理解。该解法也细节准确，计算简单明了，说明做题者对几何知识的掌握较为熟练。需要注意的是，该解法的难点在于理解题目所描述的几何图形，特别是四边形和梯形的性质，需要给做题者提供清晰准确的示意图和讲解过程，才能更好地理解解题思路。由于该解法需要较高程度的几何分析能力，适合对几何图形有一定认识的学生或对几何感兴趣的学生练习使用。

总结：这道题目可以有多种解法，每种解法都有其优点和适用条件。解法一依赖正方形的对称性原理，计算过程简单清晰；解法二使用面积计算公式，强调了梯形的性质，适合初学者使用；解法三则需要对四边形和梯形的性质有一定的理解和掌握，思维性强，适合对几何感兴趣的学生使用。需要视情况和个人情况选择适合自己的解法，可以在多种解法之间切换，加深对几何图形的认识和理解。最终，学生需要通过不断的练习，掌握解题技巧，提高几何分析能力，增强理解能力，以求得有效的解题方式。

如有其它解题思路欢迎评论区分享。

本文内容由小海整理编辑！