求极值的方法及例题(求极值的三种方法)

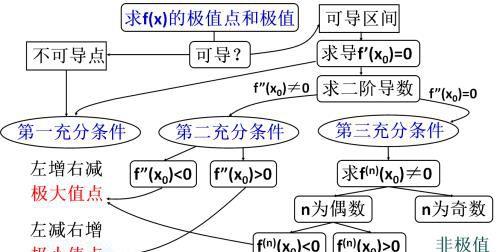
导语：求极值的方法终极总结，用思维导图分析三个充分条件的应用

求函数f(x)的极值点和极值，可以针对一点x=x0来分析。首先，我们要考虑，函数在x=x0是否可导。

1、如果x=x0是f(x)的不可导点，那么就要用极限的第一充分条件判断。函数在x0的某邻域U(x0)内，左增右减，x=x0就是f(x)的极大值点；反之，如果左减右增，x=x0就是f(x)的极小值点。否则，x=x0就不是f(x)的极值点。

(1)用定义判断，如果f(x0)比U(x0)上的任意函数值f(x)大，x=x0就是f(x)的极大值点；反之，如果f(x0)比U(x0)上的任意函数值f(x)小，x=x0就是f(x)的极小值点。

(2)用导数判断，如果在左邻域有f&39;(x)<0，x=x0就是极大值点；在左邻域有f&39;(x)>0，x=x0就是极小值点。

2、如果函数在x=x0可导，就求x0所在的可导区间上的导函数，并且解方程f&34;(x0)的符号性质来确定x=x0是什么极值点。

若f&34;(x0)>0，则x=x0是f(x)的极小值点；若f&34;(x0)<0, 则x=x0是f(x)的极大值点。

3、若f&34;(x0)=0, 就要运用第三充分条件来判断。对函数求高阶导数，直至f^(n)(x0)不等于0。

(1)此时，如果n是奇数，则x=x0不是f(x)的极值；

(2)如果n是偶数，那么当f^(n)(x0)<0时，x=x0是f(x)的极大值点，当f^(n)(x0)>0时，x=x0是f(x)的极小值点。

下面通过一道例题，来加深对这个知识的理解：

例：求f(x)=(x-1)^3(x+2)三次根号(x^2)的极值点.

解：f(x)在x=0不可导，f(0)=0,

当-2<x<0时, f(x)<0, 当0<x<1时, f(x)<0,

∴x=0是f(x)的极大值点.

f(x)=x^(14/3)-x^(11/3)-3x^(8/3)+5x^(5/3)-2x^(2/3),

f&39;(x)=0时, x=1, 或x=(-17+3根号57)/28, 或x=(-17-3根号57)/28，

f&34;(1)=0, f&34;((-17-3根号57)/28)>0, 【可以用近似数来检验，降低难度】

所以x=(-17+3根号57)/28和x=(-17-3根号57)/28都是f(x)的极小值点.

又f&39;(1)≠0, ∴x=1不是极值点. 【并不需要求导函数就可以判断，因为如果f&39;(1)=0，则f(x)有因式(x-1)^4或没有因式(x-1)^3】

综上, f(x)有极大值点x=0，以及极小值点：x=(-17+3根号57)/28和x=(-17-3根号57)/28.

函数的图像大致如上图.

现在您对求极值的方法，完全掌握了吧！

本文内容由小珊整理编辑！