多边形的切角规律(多边形剪角问题)

导语：初中平面几何多边形中的砍角问题（中考必备，家长收藏）

在小学和初中数学学习的过程中，经常会出现这样一个问题，一张课桌如果砍掉其中一个桌角，课桌还剩下几个桌角，很多学生不假思索的回答剩下3个桌角，也有同学略有所思的回答也可能是5个，那答案究竟是什么呢？针对这一类问题怎么解决呢？

一、我们通过下面的例题去寻找答案：

例：一个多边形截去一个角后，形成新多边形的内角和为2340°,则原多边形的边数为（ ）

A.15 B.16

C.13或15 D.14或15或16

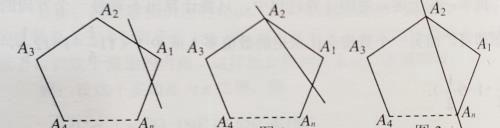
分析：如图，此类问题有三种情况：

1.如图1,新多边形的边数比原多边形多一个；

2.如图2,新多边形的边数与原多边形的边样多；

3.如图3,新多边形的边数比原多边形少一个。

解：设新多边形的边数为n,则有

(n-2)×180°=2340°,

解得：n=15.

..原多边形的边数可能为14、15和16.

二、规律总结

多边形的砍角问题，有三种情形：

1.若不经过任何一个顶点，则边数多一个；

2.若经过一个顶点时，边数不多不少，与原来相同；

3.若经过两个顶点，则边数少一个.

以后遇到这类问题同学们就应该能够轻松应对了吧，更主要的是要通过这个问题学习发散思维，从多个维度去考虑和解决问题。

本文内容由小思整理编辑！