考研数学一压轴一般是(考研数学有所谓的压轴题吗)

导语：考研数学压轴大题，考数一和数三的同学看过来，花两分钟搞清楚概率压轴题

概率是数一和数三的同学都要考的。参数估计作为考研概率的最后一个考点，也是近几年的必考题目。必然会出现在整张试卷的最后一道大题中，分值11，压轴出场。16年数一的一道填空题考查了区间估计，分值4分，17年这个知识点在数一和数三中都是考查了一道大题。所以今年参数估计这个考点的位置仍然不可动摇。参数估计包括矩估计和极大似然估计，另外考数一的同学要注意，数一还要考查区间估计，包括单个正态总体的均值和方差的区间估计、两个正态总体的均值差和方差比的区间估计。

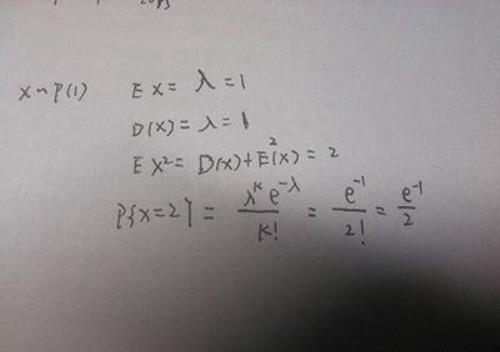
概率的题型比较固定，也是数学三门课中最好拿分的，同学们如果能掌握住考试常见题型和解题的基本方法，就能胸有成竹，每年这一门拿满分的同学很多，千万不可以掉以轻心。

一、矩估计的基本思想：

由大数定律可知样本矩、样本矩的连续函数依概率收敛于相应的总体矩、总体矩的连续函数，可由此建立总体分布中未知参数满足的方程或方程组，解之可得总体未知参数的点估计。这种构造点估计量的方法称为矩估计法，求得的点估计称为矩估计量（值）。具体步骤如下：

1、构建未知参数的方程，通过总体的原点矩来构造。

2、解方程，解出未知参数。

3、用样本矩代替总体矩，得未知参数的矩估计量（值）。

二、极大似然估计的基本思想：

样本发生的可能性最大原则--即对未知参数进行估计时，在未知参数的变化范围内选取使“样本取此观测值”的概率最大的参数值作为未知参数的点估计。这样得到的矩估计值为最大似然估计值，相应的量为最大似然估计量。具体步骤如下：

1、构造似然函数。注意：离散总体和连续总体的似然函数不同。

2、取对数。

3、求导数找驻点得估计。

如果似然方程无解，则必有导数大于或者小于0，此时只有在未知参数的变化范围内找其右边界点或左边界点即可。估计量的三大评选标准：有效性、一致性、无偏性，掌握概念即可，无偏估计考查的比较多。

总结来说：造似然求导数，找驻点得估计。

三、参数的区间估计：

这一部分数三的同学是不考的，数一的同学要了解区间估计的概念，掌握求置信区间的方法。求置信区间的步骤：

1、选枢轴量定分布。

2、构造大概率事件得不等式。

3、解不等式得置信区间。

以上就是数一和数三对参数估计部分的全部考点，希望同学们可以理解思想并且熟练掌握方法步骤，达到熟练解题的要求。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小奈创作整理编辑！