概率密度到底是什么意思(概率密度的定义)

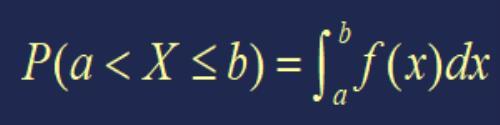
导语：概率密度到底是个什么东西

概率密度：

若存在非负可积函数 f(x), 使随机变量X取值于任一区间 (a, b] 的概率可表示成

图1

则称 X为连续型随机变量， f(x)为 X 的概率密度函数，简称概率密度或密度。

对 f(x)的进一步理解：

图2

X的概率密度函数f(x)在 x 这一点的值, 恰好是X 落在区间 [x , x +△x]上的概率与区间长度△x 之比的极限。

如果把概率理解为质量，f (x)相当于物理学中的线密度。

图3

图4

从以上分析可以得出结论：

1：概率密度是概率的变化率；

2：概率密度在一个时间段中的积分就可以得出概率。

那么，现实中能不能找到一个具体例子用来理解概率密度这个概念呢？

以打靶为例：

从图4可以看出，分布函数是一个概率，那么，概率密度到底是什么呢？

我们假设，现在有很多人对着同一块靶进行设计，每过一段时间统计射中了多少次，那么，这个随着时间变化的射中的次数就是分布函数F（x）;为了与概率密度函数f（x）相对应，我们假设每个时刻进行射击的人数是随着时间的变化而变化的，从而每个时刻击中靶的次数也是变化的，那么，这个次数就应该相当于概率密度函数f（x）。由此可以看出，一段时间内，总的射中次数,也就是概率F(x)，是和这段时间内每个时刻的射中次数，也就是概率密度函数f（x）有关的。

上面的例子还说明，F（x）本来是用来表示概率的，是一种不确定性事件，但在这个例子里面，它却具有了某种确定性的性质：它会随着时间的增加而增加（对f(t)积分）。比如，经过一段时间以后，F（x）=0.8，那就表示随着一段时间内不同的人数进行射击以后，假设总共射击了1万次，其中射中了8000次。

同时，因为概率密度函数必须满足条件

图5

这就意味着，每个射击者，其射击的命中率不能为0，要不然上图的积分永远也不会为1；而且这个命中率也不是f(x),因为f(x)表示的是某个时刻射中的次数；也不是F（x），因为F（x）表示的是一段时间内所有进行射击的人员总的命中率。因此，我们只能认为，进行射击的每一个人都有一个我们不知道的命中率，而且这个命中率应该相同，因为f(x)只能表示某个时刻所有人变化的射中次数，无法再表示每个人变化的命中率。

从上述分析可以看出，因为每个人的每次射击可以看作是一次随机试验，因此

概率密度函数f（x）似乎可以认为是进行随机试验的次数，这个随机试验是有一个出现目标样本的概率的。

因为概率密度函数是对于连续型随机变量来说的，为了模拟这个实数，我们可以假设那块目标靶位于银河系的中心，所有参加射击的人可以在太空中任何位置站立，以一个相同的命中率对着目标靶进行射击，并且那些人数随时间变化而变化。因为空间的无限性导致人数可以无限，这样大概就相当于连续的实数了。

f(x)能不能认为是同一个人在进行射击，但这个人的命中率是随着时间而变化的，也就是f(x)?从而F(x)表示的是这个人射击了一段时间以后的总的命中率？似乎也是可以的，但我们知道，概率不能大于1，但概率密度可以无穷大（对应积分区间无穷小），而且概率是一个测度，也就是这个命中率 f(x) 是包括有理数和无理数的，但命中率似乎只能是一个有理数。前面例子中的人数似乎也是有理数，但由于空间的无限性，似乎我们可以认为这个人数可以包括无理数，因为某个时刻的人数可能没人算得清。

至于图3中最后一句话是什么意思，本人不理解，欢迎讨论。

本文内容由快快网络小思创作整理编辑！