形象化表示复数的乘法口诀(形象化表示复数的乘法算式)

导语：形象化表示复数的乘法

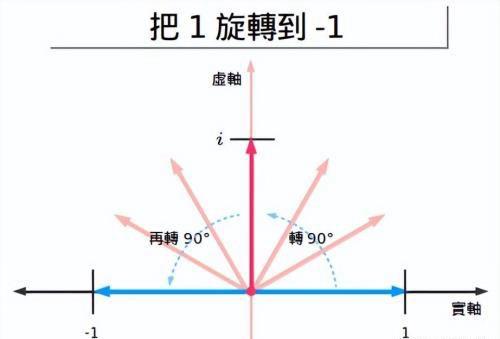
把复数看作是旋转令人茅塞顿开！

i是-1的平方根，一个存在于不同维度的数！一旦把它想通了，我们就可以把复数的旋转与乘法联系起来。

1 怎么会这样

这里有一个经常被提到的用来解释为什么复数相乘就是角度相加的阐述。

首先，把复数写成极坐标系下的形式（弧度或角度）：

接下来，进行乘法运算，实部与虚部分别进行运算：

最后，注意到它们正好符合三角函数的和差化积公式：

这样你就得到了想要的结果！

2 为什么会这样

首先，让我们看看乘法都做了些什么：

· 普通乘法（“乘以2”）将一个数按比例缩放（让它变大或变小）

· 虚数乘法（“乘以i”）将你旋转90度

如果我们在一个复数中把这些结合起来呢？比如说乘以（2+i）表示“把数翻倍——呃，然后再加上一个垂直旋转”。

一个简单的例子：

4·(3+i)＝4·3+4·i＝12+4i

这就是说，原来的数（4），放大三倍（4×3），然后再进行旋转（+4i）。再一次的，如果我们只需要旋转，我们只需乘以“i”。如果我们需要缩放只需要乘上一个普通的数字。一个复数（a+bi）可以同时实现以上两种效果。

3 形象化表示复数乘法

对于一个实数（4）乘以一个复数（3+i）来说，很简单。那么如果是两个复数相乘呢，比如说：（3+4i）×（2+3i）

看到了“原来的复数缩放后的版本（2）与旋转后的版本（3i）相加”。终点就表示一个新的复数。

但是……更喜欢另一个解释！以下就是详细说明：

不再是根据角度把乘法分开进行运算，沿着路径我们把每一部分分别相加，终点与起点不变！

4 角度怎么办呢

啊，对，还有角度。好像我们是把角度加起来了，但是我们能肯定吗？

最终的结果（蓝色的虚线）跟把角度单独相加的结果是否一致呢？

在之前的解释中，从（3+4i）开始，加上（2+3i）后得到最后的角度。

经过乘法运算以后，从一个缩放后的三角形（2倍大）开始，然后加上了另一个缩放后的三角形（乘以3i）。即便如此它也是变大了，相似三角形对应的内角角度相同——它们只是大小不同而已（先不必关心面积的变化）。

缩放了原来的三角形（但是没有改变角度），然后“加上了”另一个缩放后的三角形（同样没有改变角度），所以结果是相同的！

免责声明:本文由原创用户编辑投稿，若来源犯您的合法权益,请与我们取得联系，我们更正修改。2023年04月08日由小心整理编辑！