变态跳台阶问题(跳台阶dp)

导语：「每日一算」跳台阶与变态跳台阶

基础：

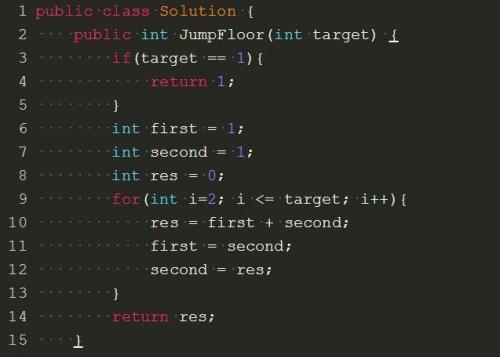
一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法（先后次序不同算不同的结果）。

这道题一开始可能很难找到头绪，但只要仔细观察就能发现：f(n) = f(n-1)+f(n-2)

这是什么意思呢？如果我们从最后一阶台阶看，那么它只能是由跳一次和跳两次得来的，所以第n阶台阶的跳法，是第n-1阶台阶加上第n-2阶台阶的跳法之和

再看第一阶和第二阶和第三阶，发现跳法分别是1,2,3，从这儿就可以看出这个问题实际上就是一个斐波那契数列的问题

代码如下：

进阶：

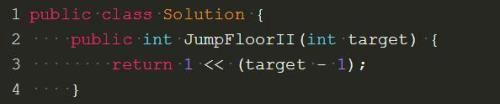
一只青蛙一次可以跳上1级台阶，也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。

这道题在上一道题的基础上变得复杂了，但是也是用上面那一道题的思路。依旧是从最后一阶梯来看：f(n) = f(n - 1)+ f(n - 2)+....+f(n - n)，这儿用到数学上的推导思想来看看倒数第二个阶梯的跳法由什么决定：f(n - 1) = f(n - 2)+f(n - 3)+.....+f(n - n)，则f(n) = f(n - 1)+f(n - 1)。

化成这种形式的话，这道题就很简单了，直接贴代码：

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小梓创作整理编辑！