两次相似题目(相似可以得出两边相等吗)

导语：两道相似的做功易错题

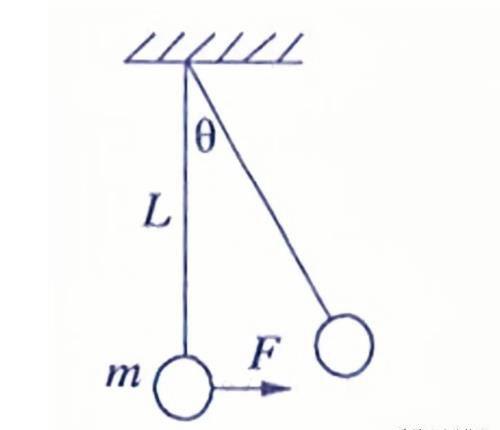
例1：如图所示，

原来质量为m的小球用长L的细线悬挂而静止在竖直位置，用水平拉力F将小球缓慢地拉到细线与竖直方向成θ角的位置的过程中，拉力F做功为:（ ）

A.FLcosθ

B. FLsinθ

C. FL（1-cosθ）

D. mgL（1-cosθ）

当F缓慢地将小球拉到细线与竖直方向成角的过程中，速率不变，动能变化量为零，由动能定理可得:

Wғ+Wɢ= △Eₖ=0

而高度变化为:h＝L（1-cosθ）

Wɢ=-mgh

所以拉力做功为:Wғ＝mgL（1-cosθ）

【变式】例：如图所示，

细线的一端固定于O点，另一端系一小球在水平拉力F作用下，小球以恒定速率在竖直平面内由A点运动到B点.在此过程中拉力的瞬时功率的变化情况是（ ）

A.逐渐增大

B.逐渐减小

C.先增大，后减小

D.先减小，后增大

【解析】如图所示，

小球的速率保持恒定，小球做匀速圆周运动（并非平衡状态），小球的重力，水平力F，绳子的拉力T的合力方向必定指向圆心.

F＝mgtanθ

Vғ＝ vcosθ

P＝F·Vғ＝mgvsinθ

由A到B角度θ逐渐增大，因此P也逐渐变大.

或者这样分析：如图所示，

小球速率保持不变，切向力为零，mgsinθ=Fcosθ⇒F=mgtanθ

Vғ＝ vcosθ

P＝F·Vғ＝mgvsinθ

由A到B角度θ逐渐增大，因此P也逐渐变大.

【另解】

绳子拉力与速度垂直，始终不做功。

∵Wғ+Wɢ= △Eₖ=0

∴Pɢ+Pғ=0

Pɢ=mgvcos［（θ+π/2）］=

-mgvsinθ

Pғ=mgvsinθ

由A到B角度θ逐渐增大，因此P也逐渐变大.

例2：如图所示，

原来质量为m的小球用长L的细线悬挂而静止在竖直位置，用水平恒定拉力F将小球拉到细线与竖直方向成θ角的位置的过程中，拉力F做功为:（ ）

A.FLcosθ

B. FLsinθ

C. FL（1-cosθ）

D. mgL（1-cosθ）

因为F是恒力，可以直接应用恒力做功公式：

W=F·l·cos（θ/2）=F·L·2Lsin（θ/2）·lcos（θ/2）=FLsinθ

☞①缓慢移动可以认为处于平衡状态，而匀速率运动不一定是平衡状态。

②若F是恒力，小球不可能匀速率运动，小球匀速率运动F一定是变力。

③注意比较两题的差别。

本文内容由小纳整理编辑！