二次函数的动点线段和短问题(中考数学二次函数动点问题)

导语：初中数学，中考二次函数中动点最短路径思路，双动点模型问题

二次函数中动点引起的最短路径及图形存在性问题

最短路径思路点拨： 两点之间，线段最短；

双动点模型

P是∠AOB内一点，M、N分别是边OA、OB上动点，求作△PMN周长最小值.

作图方法：作已知点P关于动点所在直线OA、OB的对称点P’、P’’，连接P’P’’与动点所在直线的交点M、N即为所求.

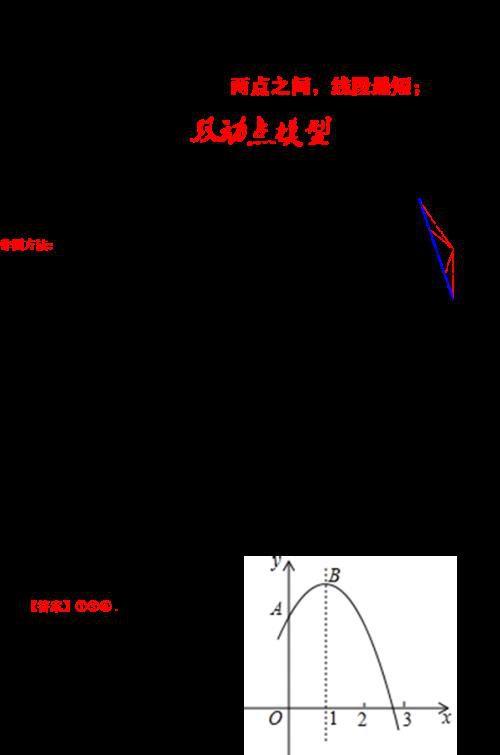
（中考题型）如图，抛物线y＝﹣x2+2x+m+1（m为常数）交y轴于点A，与x轴的一个交点在2和3之间，顶点为B．

①抛物线y＝﹣x2+2x+m+1与直线y＝m+2有且只有一个交点；

②若点M（﹣2，y1）、点N（1/2，y2）、点P（2，y3）在该函数图象上，则y1＜y2＜y3；

③将该抛物线向左平移2个单位，再向下平移2个单位，所得抛物线解析式为y＝﹣（x+1）2+m；

④点A关于直线x＝1的对称点为C，点D、E分别在x轴和y轴上，当m＝1时，四边形BCDE周长的最小值为。

其中正确判断的序号是．

【答案】①③④．

本文内容由小竹整理编辑！