勾股定理求短路径方法技巧(勾股定理的短路径问题解题思路)

导语：八年级下学期数学，巧用勾股定理求最短路径的长，四种解题技巧

八年级下学期数学，巧用勾股定理求最短路径的长，四种解题技巧。几何最值问题是难点所在，我们借助勾股定理，将军饮马模型，垂线段最短，两点之间线段最短等知识点进行解题。

01比较最短

通过计算比较解最短问题，题目中给出几种方案，按照每种方案的要求，求出最值，然后进行比较。

例题1：如图，学校有一块长方形花圃，有极少数人为了避开拐角走“捷径”，在花圃内走出了一条“路”．他们仅仅少走了（ ）步路（假设2步为1米），却踩伤了花草．

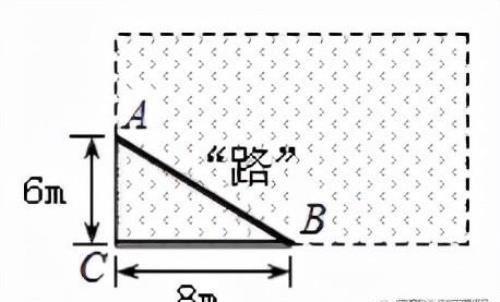
分析：求少走的步数，其实就是比较AB和AC+CB的大小关系，可利用勾股定理求出线段AB的长度，然后进行比较。

解：由题意可得：AB=10（m），

则AC+BC-AB=14-10=4（m），

故他们仅仅少走了：4×2=8（步）．

此题主要考查了勾股定理的应用，正确应用勾股定理是解题关键。

02用平移法求最值

平面图形，将分散的条件通过几何变换(平移或轴对称)进行集中，然后借助勾股定理解决，

例题2：如图，已知∠B=∠C=∠D=∠E=90°，且AB=CD=3，BC=4，DE=EF=2，则AF的长

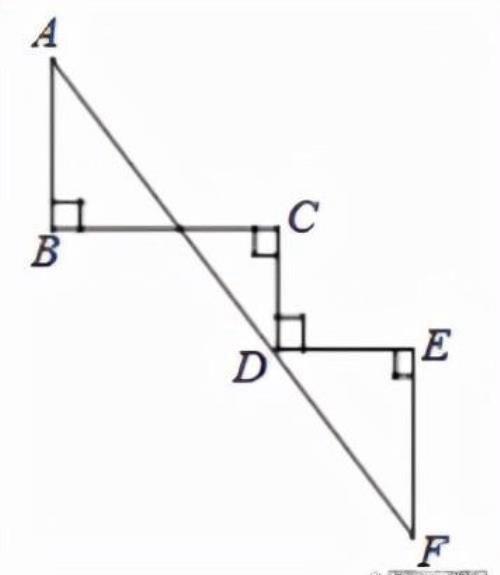
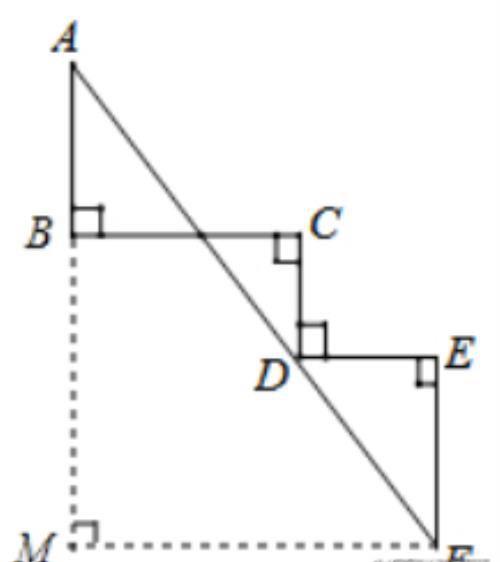
解：过F作FM⊥AB交AB的延长线于点M，

则AM=AB+DC+EF=8，FM=BC+DE=6，

在Rt△AMF中，∵AF^2=AM^2+FM^2，

∴AF=10．

本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键。

03用对称法求最值

例题3：如图所示，正方形ABCD的边长为8，M在DC上，且DM=2，N是AC上的一动点，求DN+MN的最小值．

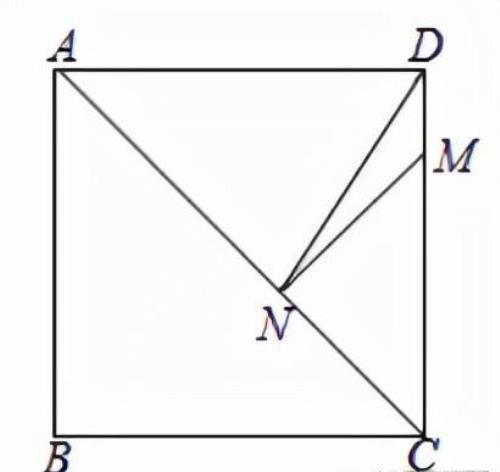
分析：要求DN+MN的最小值，DN，MN不能直接求，可考虑通过作辅助线转化DN，MN的值，从而找出其最小值求解。

解：如图，连接BM，

∵点B和点D关于直线AC对称，

∴NB=ND，则BM就是DN+MN的最小值，

∵正方形ABCD的边长是8，DM=2，

∴CM=6，∴BM=10，

∴DN+MN的最小值是10．

本考查正方形的性质和轴对称及勾股定理等知识的综合应用，解题的难点在于确定满足条件的点N的位置：利用轴对称的方法．然后熟练运用勾股定理。

04用展开法求立体图形中最值

立体图形，将立体图形展开为平面图形，在平面图形中将路程转化为两点间的距离，然后借助直角三角形利用勾股定理求出最短路程(距离)。

例题4：如图，一个长方体形的木柜放在墙角处（与墙面和地面均没有缝隙），有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处．当AB=4，BC=4，CC1=5时，则蚂蚁爬过的最短路径的长

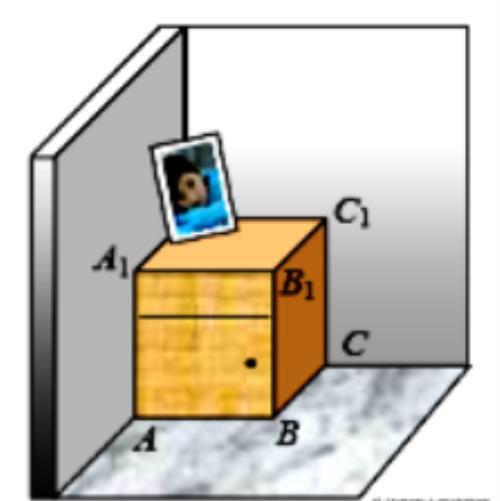
分析：求出蚂蚁沿着木柜表面经线段A1B1到C1，以及蚂蚁沿着木柜表面经线段BB1到C1的距离，再进行比较即可．

此题主要考查了长方体展开图的对角线长度求法，这种题型经常在中考中出现，也是易错题型，希望能引起同学们的注意。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小欣创作整理编辑！