换元法求极限的条件(换元替代法)

导语：换元法和替换法求极限（三）

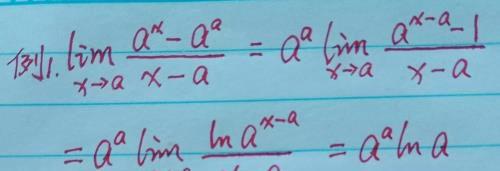
本篇文章是上两篇同名文章的续篇，有兴趣的可以先看前两篇。

换元和替换法求极限方法非常好，也很锻炼思维，本篇文章不用洛必达法则，主要目的是深入领会换元和替换法思想，并达到切实掌握的目的。

一、替换法

看例1

a^（x－a）－1替换成ln[a^（x－a)]根据是ln（x+1)～x（x→0），熟练利用这个等价无穷小可以快速进行ln（x+1)与x相互替换。

接着看例2

关键一步是利用ln（sinx+1)～sinx（x→0)，把前者替换成后者。

下面两道例题综合应用换元法和替换法，其实换元实质主要是方便求解，看例3。

lny～y－1（y→1)， 可以通过简单变形，lny＝ln（y－1+1)～y－1（y→1)，就好理解了。

最后看例4，可能有点难，其实主要替换根据和上面3题相同，ln（siny+cosy)～siny+cosy－1（y→0）。

总结一下，本文所用替换依据：ln（x+1)～x（x→0）。

最后鲜花送给所有阅读我文章的朋友，我自己院子里的仙人球花。

前两篇同名文章里面的花也是我自己院子里的花，名字叫凌霄花。

请朋友们多点赞，多关注！

本文内容由小余整理编辑！