长方形中四个小长方形面积的一个相等关系是什么(四个长方形面积之间的关系)

导语：长方形中四个小长方形面积的一个相等关系

长方形面积一个有趣的性质

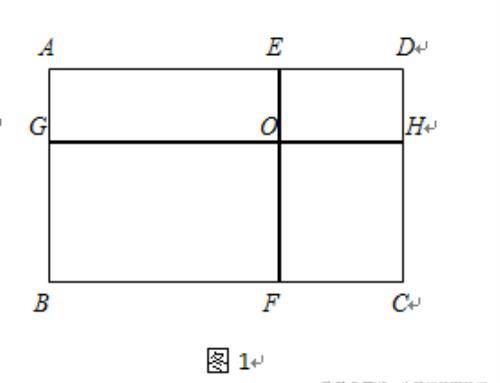
如图1，经过长方形ABCD内一点O，分别与两组对边平行的两条直线EF和GH将长方形ABCD分成的四个小长方形AEOG、BGOF、CFOH、DHOE中，设它们的面积依次为SA，SB，SC，SD，则SA•SC=SB•SD.

即相对两个小长方形面积的乘积相等。

证明：设AE=GO=BF=a，ED=OH=FC=b，AG=EO=DH=c，GB =OF =HC=d，则

SA•SC=ac•bd=abcd，

SB•SD=ad•bc=abcd，

所以SA•SC=SB•SD.

事实上这个结论对于平行四边形也成立，对于任意四边形被对角线分成的四个三角形也成立。

运用这个结论求解有关长方形面积问题异常简便。请看：

例1 如图2，三个小长方形的面积图中所示，第四个小长方形的面积S=_________。

解：由上述结论，得

14S=6×35，所以S=15.

例2 如图3，直角三角形ABC中，∠A=90°，正方形AEFG的顶点E、F、G分别在AB、BC、AC边上，如果△BEF的面积为8，△CFG的面积为18，则正方形AEFG的面积为_________。

解：以AB、AC为一组邻边作长方形ABMC，延长EF交MC于H，延长GF交BM于N。则

长方形BEFN的面积为16，长方形CGFH的面积为36。设正方形AEFG的面积为S。

因为△BMC的面积=△ABC的面积，S△CFG=S△CFH，S△BFE=S△BFN，

所以长方形MNFH的面积=正方形AEFG的面积=S，

所以S^2=16×36，

所以S=4×6=24.

事实上，将正方形AEFG换作长方形结论也是成立的。

本文内容由小里整理编辑！