结构力学平面体系的几何组成分析(结构力学几何图形分析)
导语:走进土木工程——结构力学的平面体系几何构造分析(2)
基本概念:
体系的自由度:指完全确定体系位置所需要的独立坐标(直角坐标、几何参数)的数目。
几何约束:对非自由系各部分的位置所加的几何学上的限制。
复铰:联结两个以上刚片的铰。
必要约束:使体系成为几何不变而必须的约束。
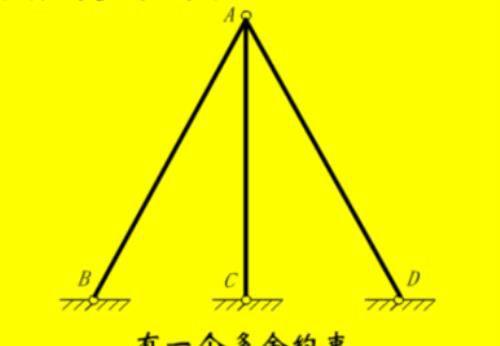
多余约束:必要约束之外的约束。
体系的自由度=各组成部分总的自由度数-体系中的必要约束数,若为0,则体系几何不变。这是几何不变的充分条件。(但必要约束并非都可以直观判定,故引入计算自由度W的概念)
计算自由度:计算自由度W =各组成部分总自由度数-全部约束数(可能包括多余约束)。当W≤0,则几何不变;若W>0,则体系一定是几何可变。(即W≤0是几何不变的必要条件,不充分!我们更需要充分条件——两刚片、三刚片规则)
体系的静定性:在任意荷载下全部内反力可否由平衡条件确定。
重点内容:
一个动点有2个自由度。
一个刚片在平面内有3个自由度。
一根链杆相当于1个约束,可以减少1个自由度。
一个铰相当于2个约束,可以减少2个自由度。
联结n个刚片的复铰可以当作n-1个单铰,减少2(n-1)个自由度。
一个刚结点相当于3个约束,可以减少3个自由度。
同理,联结n个刚片的复刚结点相当于n-1个单刚结点,可以减少3(n-1)个自由度。
小总结:
联结方式
相当于几个约束
减少自由度
链杆
1
1
铰
2
2
刚结点
3
3
复铰
2(n-1)
2(n-1)
复刚结点
3(n-1)
3(n-1)
两刚片规则:两个刚片间用不相交于一点也不相平行的三根链杆相联,其内部是几何不变的,并且没有多余约束。[另一种表述:两个刚片间用一个铰(实铰或虚铰)和一根不通过该铰的链杆相联,其内部是几何不变的,并且没有多余约束]
三刚片规则:三个刚片用不在一直线上的三个铰两两相联,其内部是几何不变的,并且没有多余约束。
基本组成规则的应用技巧:一元体二元体的增减、链杆↔刚片
几何构造与静定性:
本文内容由小姿整理编辑!