初中数学几何常见辅助线作法口诀(几何题中辅助线应该是什么线)

导语：中考几何压轴 72 辅助线法则 辅助圆，算术平均 几何意义与辅助线

中考几何压轴 72 辅助线法则 辅助圆，算术平均 几何意义与辅助线

这一系列，不限专题，解析系列经典几何题，提高几何分析解决问题能力。

题79. 《辅助圆·算术平均·几何意义》

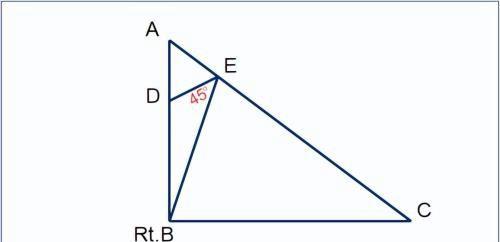
如图，△Rt.ABC中，∠ABC＝90°， BC＝4；D、E分别是AB、AC上的点，BD＝2，∠BED＝45°，若AC－AB＝2AE，求线段AB的长度。

〖一般性提点〗

[1]. 本题经典再现了求线段长度的一般方法。

<1>. 角度/线段分析，设置适当的未知数：角度分析的根本目的，是暨此获得线段信息。

<2>. 根据几何原理，建立关联线段表达（含未知数）：综合性强，各种必要的几何原理。

<3>. 基于几何原理，建立关于未知数的方程并求解方程：主要是Rt.三角形、相似三角形。

[2]. 圆：简约强大的角度分析手段

之所以如此，关键在于角度和弧长的正比关系。圆上的角，就好比直线上的点：

一旦角度和圆产生关系（其射线或其反向延长线均与圆有交点），那么该角度就正比于其所对弧和或差之半：圆内角取和，圆外角取差。

所以，辅助圆和辅助线，有着同等重要的地位，也是各位学友容易忽略之所。

详细参考题目分析。

〖题目分析〗

本题关键在于∠BED＝45°，AC－AB＝2BE 两个条件怎么用。

[1].45°角：怎么利用

题设45°角关联的辅助线，一般是补全等腰直角三角形，本题明面上缺乏着力点，但别忘了一个隐藏的点：外接圆圆心O。特殊的角度，弦与圆心构成特殊三角形：45°对应等腰Rt.三角形；30°对应正三角形等，如图。

[2]. AC－AB＝2AE的含义

该关系，隐藏着中点信息（算术平均的几何意义）。意识到这一点是确定解题路线的关键。

代数中：

m－n，m，m＋n:

m＝[(m＋n)+(m－n)]/2

m 称为是(m－n)、(m＋n)的算术平均。易知：(m＋n)－(m－n)＝2n。

算术平均的几何意义就是线段的中点。

若灵活掌握了这个要点，本题就不难了。结合本题，CE就是AC＝(m＋n)，AB＝(m－n)的算术平均（其中，AE＝n）：

CE＝AC－AE＝AB＋AE

结合本题，在几何上，就是延长EA至H，使得AH＝AB，则点E就是线段CH的中点。

这就是AC－AB＝2AE告诉你要做的事情。

<1>. 作△BDE外接圆O，O为圆心；圆O与AC、BC的交点（B、E之外）分别是G、F；

<2>. 延长CA至H使得AH＝AB，连接BH；由题设AC－AB＝2AE，易知，E是CH之中点；△ABH是等腰三角形；

[3]. 角度线段分析

显然，求AB就是求AD，设AD＝λ；目标方向是用λ表达AC；这样，在Rt.△ABC中，基于勾股定理，可建立关于λ的方程。

圆O将线段AC分为三段，因此，可以分别寻求这三段的表达式。

接下来的角度线段分析，没有太大难度，要的是定力和眼力。

<1>.连接OF

∵ DBF＝90°，∴ DF是圆O的一条直径，且∵∠BOD＝90°，∴∠BDO＝45°，∴ Rt.△DBF是等腰三角形：

BF＝BD＝2；

则 CF＝BC－BF＝2；

∴ F是BC的中点；（这样，加上E，有了两个中点）

<2>. EG、CG、AE：

AC三段中，和圆关联最密切的是EG，所以先关注EG的表达；

记BH与圆O的交点为K；关联角度标记参考图：

EF是△BCH的中位线：EF∥BH；

∴ 弧EDK＝弧BF，其上的圆周角＝45°；

即θ＋β＝45°；

∵ △ABH是等腰三角形，又EF∥BH；

∴ ∠CEF＝∠AHB＝∠ABH＝θ；

而∠DFE＝∠DBE＝β（同弧圆周角）；

考察直径DF上的弧DEGF：

∵ 弧 DE、FG上的圆周角之和为45°；

∴弧EG上的圆周角＝45°；即：

弧EG＝弧BF（＝弧BD），得到系列相等线段、圆周角度；以及关联平行线：

∴结果① ：EG＝BF＝2；

结果②：∠CEB＝∠CBE，△CBE是等腰三角形；

结果③：连接FG∥BE，G为CE中点：CG＝EG＝2；

结果④：连接BG∥DE，且△ABG为等腰三角形，

∴ △ADE也是等腰三角形：AE＝AD＝λ；

[4]. 在Rt.△ABC中，由勾股定理建立关于λ的方程并求解，这就非常简单了，结果是：

λ＝1；

∴ AB＝BD＋AD＝3.

本文内容由小茹整理编辑！