初中数学黄金分割比(黄金分割比例数学题)

导语：巧用黄金分割比，解中考数学关于圆的压轴题，最爽、最解压的解法

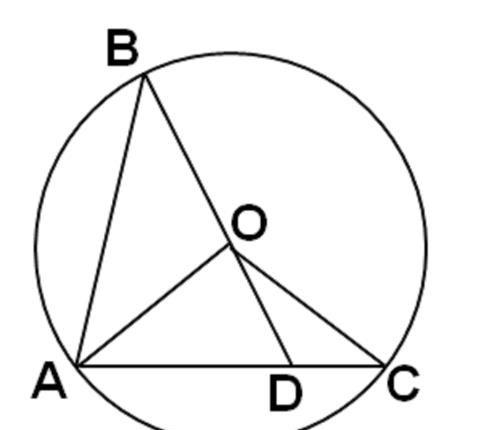
这道中考数学关于圆的压轴题，是朝着难题的方向去设计的，就算能解决，也会比较繁琐。但经老黄详细拆解后，却变成了一道特别简单的压轴题。题目是这样的：

如图，⊙O的半径长为1，AB，AC是⊙O的两条弦，且AB=AC，BO的延长线交AC于点D，联结OA，OC.

(1)求证△OAD∽△ABD；

(2)当△OCD是直角三角形时，求B，C两点的距离；

(3)记△AOB，△AOD，△COD的面积分别为S1，S2，S3，如果S2是S1和S3的比例中项，求OD的长.

【第(1)小题是送分题，只要证明∠ODA=∠ADB，加上一组公共角，就有△OAD∽△ABD.】

(1)证明：∵AB=AC, ∴∠AOB=∠AOC,

又OA=OB=OC ∴∠OAD=∠ABD, 【这一步绝大多数人会通过证明△AOB和△AOC全等，来得到这个结论。但老黄直接跳过全等的证明，运用的是“顶角相等的等腰三角形底角也相等”的定理。】

又∠ODA=∠ADB, ∴△OAD∽△ABD.

【第(2)小题画图的能力远比解题的能力重要，只要能画出图来，答案自然就出来了。】

解：(2)连接BC, 如图1, 当∠ODC=90度时, AD=CD，

所以BC=AB=AC=根号3OC=根号3. 【这里运用了等边三角形外接圆半径与边的数量关系】

【有些地方给的答案，只有这种情形，但老黄探究之后，发现还有一种情况，如下：】

如图2, 当∠COD=90度时, BC=根号2OC=根号2.【这里运用了等腰直角三角形三边的数量关系】

【第三小题按理应该是最难的，但是只要你记得黄金比例的比值，就可以轻松解决了】

(3)由(1)可知，S△AOC=S1, 【即三角形AOC和三角形AOB是全等的，因此面积相等】

由S2^2=S1·S3, 知AD^2=AC·CD, 【这里三个三角形的高相同，所以面积的比例关系，等同于底边的比例关系，可以看到，AD就是黄金比例的比例中项】

从而有AD=(根号5-1)AC/2=(根号5-1)AB/2，

又AB/OA=AD/OD，【这是(1)中的相似三角形的边的比例关系】

∴OD=AD·OA/AB=(根号5-1)/2.

怎么样，这样解中考数学压轴题，是不是很爽，很解压呢？不过这里面用到了好几个平时很少用到的知识点，所以中考的好成绩，几乎都是平时积累来的。那种企图短时间内就提升中考成绩的想法，是不可取的哦。

本文内容由快快网络小曲整理编辑！