几何特性中的比例如何应用出来(几何比例关系)

导语：几何特性中的比例如何应用

比例关系是我们数学中常见的一种做题方法，很多题型中都能用，能够满足关系式条件式的基本均有比例特性。如：行程问题：路程=速度×时间；工程问题：工作总量=工作效率×工作时间；经济利润问题：总价=单价×数量；几何问题等。

在几何问题里，我们应用较多的比例关系为相似比例特性，即两个相似图形若边长比为，则周长比也为，面积比为，体积比为。这里所说的相似是指两个图形形状相同但大小不同，那么我们会说这两个图形相似，最常见应用较多的即相似三角形，两个三角形对应角都相等，那么我们就可以判定这两个三角形相似。

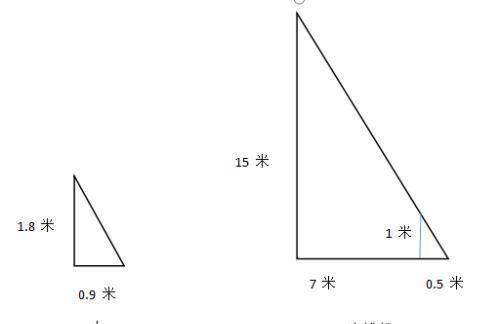
【例1】阳光下，电线杆的影子投射在墙面及地面上，其中墙面部分的高度为1米，地面部分的长度为7米。甲某身高1.8米，同一时刻在地面形成的影子长0.9米。则该电线杆的高度为：

A.12米 B.14米

C.15米 D.16米

【如图所示】

【解题思路】由题意可知，真实长度与影子长度之比为2∶1，墙面部分的影子长度投影到地面上才是该部分真实的影子长度，即电线杆的影子总长为7＋0.5＝7.5(米)，所以电线杆的高度为7.5×2＝15(米)。故本题选择C。

【例2】如下图所示，在一个正方形内画中，小两个正方形，使三个正方形具有公共顶点，这样大正方形被分割成了正方形区域甲和L形区域乙、丙。已知三块区域甲、乙、丙的周长之比为4:5:7，并且区域丙的面积为48，求大正方形的面积：

A.96 B.98

C.200 D.102

【解析】由题目可知：

第一步，观察图形，可知有大、中、小三个不同的正方形，因此三者相似；

第二步，做割补平移，因甲为正方形，将乙区域与甲区域重叠的两条边换成甲外部的两条边，周长不变，发现图形变为中正方形，同理，丙区域周长为大正方形周长；

第三步，由甲、乙、丙的周长之比为4:5:7，即小、中、大三个正方形周长之比为4:5:7，则面积之比为16:25:49；

第四步，区域丙的面积为48，区域丙面积为大正方形减去中正方形，占比为，因此24份对应面积为48，可知实际面积为比例的2倍；

第五步，求大正方形面积，根据比例关系可知其占比为49，则面积为98。

通过比例关系，能够让我们的解题过程由复杂变简单。因此，比例常用于我们的快速计算。

本文内容由小春整理编辑！