复数的几何意义及应用论文(复数的几何意义及应用例题)

导语：复数的几何意义及应用

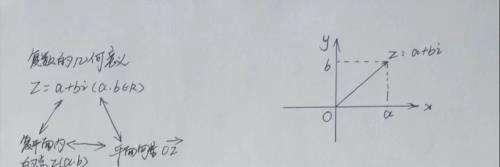
要掌握复数的几何意义，就要搞懂复数、复平面内的点以及向量三者之间的一 一对应关系，从而准确理解复数的“数”与“形”的特征。

理解了复数的几何意义，就能将标准形式的复数在复平面上用点或向量表示出来，并能将复平面上的点或向量所对应的复数用表示形式表示出来。考试中，通常与复数的四则运算一起考查。

复数z=a+bi（a，bR）复平面内点Z（a，b）平面向量OZ

例题：Z1=+i，Z2=x+yi（x，y∈R），Z1，Z2对应的向量分别是OZ1、OZ2，O为坐标原点，若≤，则的最大值是（ 3 ）

与复数加、减的几何意义有关的常用结论：

设Z1、Z2在复平面对应的点为A、B，Z1+Z2在复平面对应的点为C

（1）若=，则四边形OACB为矩形；

（2）若=，则四边形OACB为菱形；

（3）若=，且=，则四边形OACB为正方形。

本文内容由小春整理编辑！