中考数学动点产生的二次函数面积方法解题(二次函数动点面积问题的例题)

导语：中考数学，动点产生的二次函数面积，方法解析

中考数学，最后的三道压轴题，一般都会有一题考察二次函数动点。本文只是针对常考的二次函数面积问题进行解析，其它类型在以后的文章中陆续上传。解决二次函数动点面积问题，常用的方法有三种。

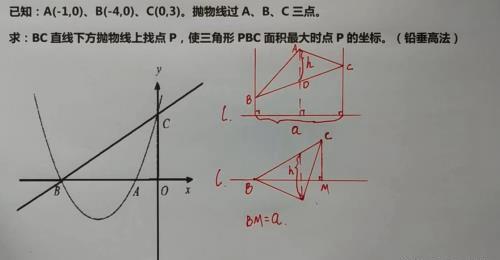
方法一，铅垂高法。如下图，a代表水平宽，h代表铅垂高，通过图形，可以看出三角形ABC的面积等于a和h乘积的一半，如果看不出来，可以自己推导一下，因为软件限制，有些数学公式和符号写不出来。

通过上图解析，我们可以看出，铅垂高的表示法是解这种题的关键。同学们可以结合我写的简略过程，进行一下总结，而且还可以知识的迁移。比如不问最大面积，而是问面积等于一个数，或者面积等于某三角形面积等类型，解法都是相同的。

方法二，平行法。平行法最关键的知识点，是平行线之间高的问题，一般这种情况都是平移高到与坐标轴交点处，最后用相似求值。如果题目如下图，还涉及到二次函数与一次函数只有一个交点问题，解决方法是联立得到一元二次方程，根据只有一个交点，利用根的判别式等于0可以解决。

上图只是给出这种解法的一种问法，还可以去问高是定值的时候求点的坐标，或者告诉我们面积的值，求其它的量。但无论什么样的问题，都是围绕这个知识点在考察，所以要求我们一定要对方法理解得非常透彻，才能应对各种变化。

方法三，矩形覆盖法。这是最容易想到的方法，但也是计算最麻烦的方法。利用面积的大减小去解决，一般不太建议使用这种方法，庞大的计算量很容易出错。

综上，二次函数动点常用的三种方法，如果能够充分理解，并且灵活运用。这类题目大多数类型都可以解决，而且这几种也包含了其它动点题需要用到的知识点，可以说是不可不学的几个基本模型。本文原创，转载请注明出处，转发随意。

本文内容由小滢整理编辑！