铅垂法求三角形面积公式(初中三角形铅垂法推导)

导语：初中数学：巧用隐圆+铅垂法，快速求解三角形面积

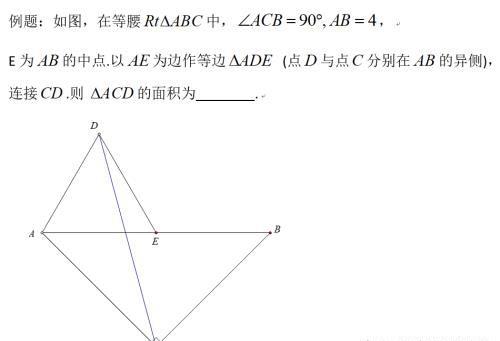
求三角形面积是初中几何很常见的问题，本文仅选取一题，只给出2种方法，聊作介绍。如图：

本题图形很“美”，出现了等边三角形+等腰直角三角形+中点，这几个很“好”的几何要素。而我们知道“直角三角形，斜边上的中线等于斜边的一半”，所以出现很多相等的线段：EA=EB=EC=ED=AD=2.并且CA=CB=2√2本题条件挖掘差不多了。

方法1：“辅助圆”解题。因为共端点（E）的几条线段EA=EB=EC=ED，所以点A,B,C,D四个点在以E为圆心的圆上。放在圆的背景之下，就可以用圆的性质来“导角”：①根据“同弧所对的圆周角相等”得∠ADC=∠B=45°；根据“圆周角等于圆心角的一半”可得∠ACD=0.5∠AED=30°，而45°和30°是我们“求之不得”的！所以这时候求面积找底找高，我们将CD作为底，作垂线AF作为高。显然CD,AF利用两个特殊三角形非常好求，几乎可以口算，漂亮！如图：

方法2：“铅垂法”。三角形面积=1/2水平宽×铅垂高。推导过程本文不作论述，用的是割补思想。如图，作DF⊥AB，显然可以把AE=2看做水平宽，把DF作为铅垂高，而DF=DG+GF.可爱的是DG,GF分别在两个可爱的直角三角形中（含有45°和30°）数值可以口算。至此本题迎刃而解，兵不血刃，如图：

当然本题还有不下于5种方法，上述两种解法精致紧凑，方便计算，题目小小能量大。

你喜欢哪种方法呢？欢迎留言评论，甚至给出更加精彩的解法。

本文内容由小梓整理编辑！