长方形abcd求阴影部分面积(求长方形阴影面积18cm16cm)

导语：“求阴影面积”专题，长方形边BD=10,DC=6,BC=8求▲DEF的面积

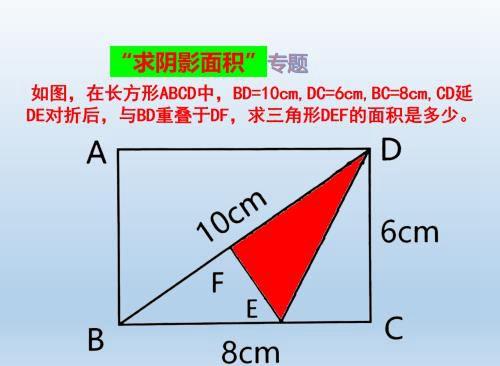
题目：如图，在长方形ABCD中，BD=10cm,DC=6cm,BC=8cm,CD延DE对折后，与BD重叠于DF，求三角形DEF的面积是多少。

解法1：设BE为x、EC为y，x+y=8。根据三角形角平分线定理，BD:DC=10:6=5:3=x:y，与x+y=8组成方程组并解之x=5(cm)、y=3(cm)。阴影=6×3÷2=9(cm²)。

解法2：利用等高三角形底的比例等于面积比例的道理，可知BEF的面积与DEF的面积比为4/6＝2/3 也就是说，三角形BCD内的三个三角形面积比为2/3/3，分做8份的话，每份为3平方厘米。阴影面积为3份＝9平方厘米！

解法3：解：由折叠图形得：DF=CD=6cm， BF=10-6=4cm，设EF=EC=x，则BE=8-x。在直角三角形BEF中，根据勾股定理得：x^2+4^2=（8-x）^2，解得x=3cm，即EF=3cm，所以三角形DEF面积=3X6÷2=9cm^2

解法4：DBC=8×6÷2=24cm^2 阴影DFE=空白DCE 阴影DFE和空白BFE同高 ∵DF=6cm，BF=4cm ∴阴影DFE : 空白BFE=6 : 4=3 : 2 设: 阴影DFE=3a，空白BFE=2a 则: 空白DCE=阴影DFE=3a 由图可知: 2a+3a+3a=24，a=3，3a=9 阴影DFE=3a=9cm^2

解法5：∵CD延DE对折后，与BD重叠于DF，∴CE＝EF又∵△DBC的面积＝△DEB的面积＋△DEC的面积：设CE＝EF为a，8×6÷2＝a×10÷2十a×6÷2，∴a＝3，∴3×6÷2＝9。

本文内容由小森整理编辑！