中考原题例说待定系数法的应用题及答案(待定系数法典型例题)

导语：中考原题例说待定系数法的应用

待定系数法是初中数学中的一种常用的解题方法，这里举例说明待定系数法的应用．

一、用待定系数法求方程（组）中待定系数的值

例1（扬州中考题）已知关于x的方程3x+n/2x+1＝2的解是负数，则n的取值范围为_______．

分析 求出分式方程的解x＝ n－2，得出n－2 <0，求出n的范围，根据分式方程得出n－2≠½，求出n，即可得出答案，本题关键是得出n－2<0和n－2≠－½，注意题目中的隐含条件2x＋1≠0，不要忽略．

解：3x+n/2x+1＝2，解方程得x＝n－2．

∵关于x的方程3x+n/2x+1＝2的解是负数，∴n－2<0，解得n<2．

又∵原方程有意义的条件为x≠－½，∴n－2≠－½，即n≠3/2．

故答案为n<2且n≠3/2．

例2（黑龙江省龙东地区中考题）已知关于x的分式方程a+2/x+1＝1的解是非正数，则a的取值范围是( )

(A)a≤－1 (B)a≤－1，且a≠－2

(C)a≤1，且a≠－2 (D)a≤1

分析 先解关于x的分式方程，求得x的值，然后再依据“解是非正数”建立不等式，并求a的取值范围，本题需注意考虑分母不为0，这也是本题最容易出错的地方．

解 去分母，得a＋2＝x＋1，

解得x＝a＋1．

∵x≤0．．且x＋1≠0，∴a＋1≤0，且a＋1≠－1，

∴a≤－1，且a≠－2，∴a≤－1，且a≠2．故选B．

二、用待定系数法确定函数关系式

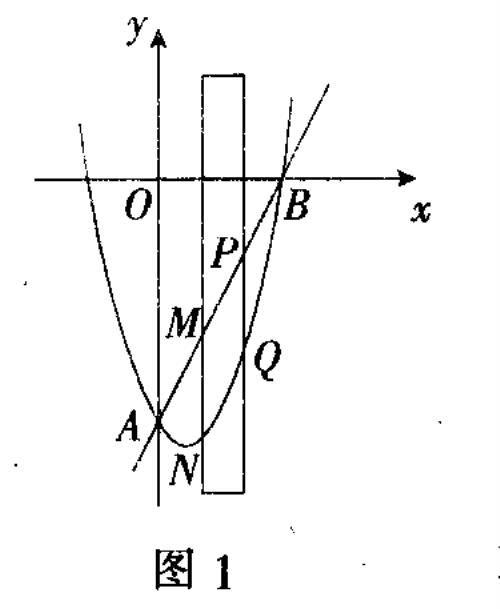
例3 （扬州中考题）如图1，抛物线y＝x²－2x－8交y轴于点A，交x轴正半轴于点B．

(1)求直线AB对应的函数关系式；

(2)有一宽度为1的直尺平行于y轴，在点A、B之间平行移动，直尺两长边所在直线被直线AB和抛物线截得两线段MN、PQ，设M点的横坐标为m，且0<m<3，试比较线段MN与PQ的大小．

分析 第(1)问利用二次函数解析式，求出A、B两点的坐标，再利用待定系数法求出一次函数解析式；第(2)问根据M的横坐标和直尺的宽度，求出P的横坐标，再代入直线和抛物线解析式，求出MN、PQ的长度表达式，再比较即可．

解 (1)当x＝0时，y＝－8；

当y＝0时，x2－2x－8＝0，

解得x1＝4，x2＝－2，

则A（0，－8），B(4，0)．

设一次函数解析式为y＝kx＋b．

将A（0，－8），B(4，0)分别代入解析式， 解得k=2,b=-8

故一次函数解析式为y＝ 2x－8．

(2)∵M点横坐标为m，则P点横坐标为(m＋1)．

∴MN＝(2m－8)－（m2－2m－8)＝2m－8－m2＋2m－8＝－m2＋4m；

PQ＝[2(m＋1)－8]－[(m＋1)2－2(m＋1)－8]＝－m2＋2m＋3．

∴MN－PQ＝（－m2＋4m，）－（－m2＋2m＋3）＝2m－3．

①当2m－3＝0时，m＝3/2，即MN－PQ＝0，MN＝PQ；

②当2m－3 >0时，3/2<m<3，即MN－PQ>0，MN>PQ；

③当2m－3<0时，0<m<3/2，即MN－PQ<0，MN<PQ．

例4 （苏州中考题）如图2，已知抛物线y＝½x²＋bx＋c（b，c是常数，且c<0）与x轴分别交于点A、B（点A位于点B的左侧），与y轴的负半轴交于点C，点A的坐标为（－1，0）．

(1)b＝_______，点B的横坐标为_______；（上述结果均用含c的代数式表示）

(2)连结BC，过点A作直线AE∥BC，与抛物线y＝x²＋bx＋c交于点E，点D是x轴上的一点，其坐标为(2，0)．当C，D，E三点在同一直线上时，求抛物线的解析式．

分析与略解 第(1)问将A（－1，0）代入y＝x²＋bx＋c，可以得出b＝½＋c；

根据一元二次方程根与系数的关系，得出xB＝－2c．

第(2)问如图3，由y＝x²＋bx＋c，求出此抛物线与y轴的交点C的坐标为(0，c)，则可设直线BC的解析式为y＝kx＋c，将B点坐标代入，运用待定系数法求出直线BC的解析式为y＝½x＋c．由AE∥BC，设直线AE，得到解析式为y＝½x＋m，将点A的坐标代入，运用待定系数法求出直线AE得到解析式y＝½x＋½．

解方程组y=½x²+(½+c)x+c,y=½x+½

求出点E坐标为（1－2c，1－c），将点E坐标代入直线CD的解析式y＝－c/2x＋c，求出c＝－2，进而得到抛物线的解析式为y=½x²-3/2x-2．

您给我转评赞，有一样就谢谢您了！

本文内容由小嫣整理编辑！