算法汉诺塔问题(算法汉诺塔问题3个答案)

导语：算法-汉诺塔

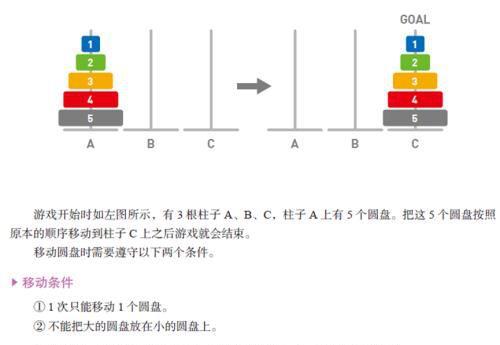
汉诺塔是一种移动圆盘的游戏。

传说: 在世界中心贝拿勒斯（在印度北部）的圣庙里，一块黄铜板上插着三根宝石针。印度教的主神梵天在创造世界的时候，在其中一根针上从下到上地穿好了由大到小的64片金片，这就是所谓的汉诺塔。不论白天黑夜，总有一个僧侣在按照下面的法则移动这些金片：一次只移动一片，不管在哪根针上，小片必须在大片上面。僧侣们预言，当所有的金片都从梵天穿好的那根针上移到另外一根针上时，世界就将在一声霹雳中消灭，而梵塔、庙宇和众生也都将同归于尽。即使是每微秒移动一次， 也需要5000世纪的时间。

规则：

证明：

数学归纳法

数学归纳法是证明某个命题关于整数n(对所有的n>=n0)成立的一种一般的方法。首先，当n为最小值n0时我们证明命题，这称为基础，然后假设对于包含再n0和n-1之间的所有值，已经证明命题成立，对于n>n0证明命题，这种方法称为数学归纳法。

根据以上内容，可知：

f(0)=0 f(1) = 1 f(2) = 3 f(3) = 7 f(4) = 15 f(5) = 31 …

好像有点规律， f(n) = 2^n -1

那么这个猜想正确吗?用数学归纳法证明一下。

证明

f(0) = 2^0 -1,

f(1) = 2^1 -1,

f(2) = 2^2 -1,都是正确的

假设n-1取代n的时候上述猜想成立，且对于n>0建立归纳，

f(n) = 2f(n-1) + 1

= 2(2^(n-1)-1)+1

= 2^n-2+1

= 2^n -1

因此，对于n来说，上面的猜想依然成立

本文内容由小莉整理编辑！