初中几何平移问题(平移的几何语言)

导语：中考几何压轴 73 几何与函数 平移的表达，45°多与半角、12345相关

中考几何压轴 73 几何与函数 平移的表达，45°多与半角、12345模型相关

这一系列，不限专题，解析系列经典几何题，提高几何分析解决问题能力。

题80. 《平移后抛物线表达式》

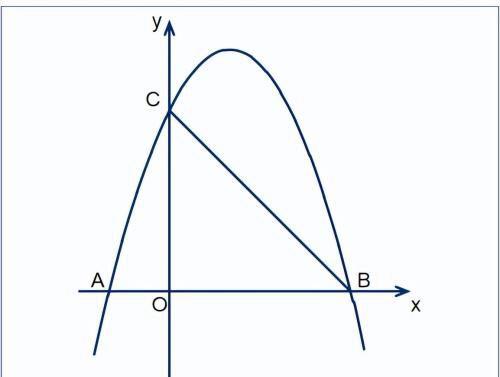
如图，抛物线y＝ax²＋bx＋3与x轴交于点A(-1,0)和点B(3,0)，与y轴交于点C，顶点为D。

[1]. 求该抛物线的表达式和顶点D的坐标；

[2]. 将抛物线沿y轴上下平移，平移后所得新抛物线顶点为M，点C的对应点为E；

<1>. 如果点M落在线段BC上，求∠DBE的度数；

<2>. 设直线ME与x轴正半轴交于点P，与线段BC交于点Q，当PE＝2PQ时，求平移后新抛物线的表达式。

〖一般性提点〗

☆ 抛物线的平移

原抛物线：y＝ax²＋bx＋c

抛物线平移，仅涉及上下平移。设平移h单位：

h＞0向上平移；

h＜0向下平移；

新抛物线：y＝ax²＋bx＋(c＋h)

点的对应：

原抛物线上的点P(m, n)，对应新抛物线上的点P´(m, n＋h)；

☆ 求角度数

肯定是特殊角，意味着特殊三角形。

<1>.由此，结合本题。猜测到所求角是45°，即可以看到正方形半角模型＋12345模型的影子。

<2>. 或者，用两点距离公式，证明△BED为等腰Rt.△BED。

本题重点是[2]<2>，详细参考题目分析。

〖题目分析〗

[1].

抛物线：y＝－x²＋2x＋3

顶点：D（1，4）

[2]. <1>. ∠DBE

易知，L(BC)：y＝-x＋3，易求得：

M(1,2), E(0,2)；

两点距离公式计算BE＝DE＝√10；BD＝2√5；且有BD²＝BE²＋DE²

∴ △BDE是Rt.等腰三角形，∠DBE＝45°；

或者（见图）：

tanα＝1/3；tanβ＝1/2；

由12345模型，α＋β＝45°

∴ ∠DBE＝90－α－β＝45°。

[2]. <2>.

只要求出平移量h＝yM－yD（＜0）

新抛物线：y＝－x²＋2x＋3＋h

由题设易知，△BPQ和△EPO都是等腰直角三角形；OP＝PE/√2；BP＝√2·PQ；

BP/OP＝(√2·PQ)/( PE/√2)＝1；即P为OB中点;

设M(1,yD＋h)，即 M(1,4＋h)

则：

E(0, yC＋h)，即E(0, 3＋h)

P(-yE,0)＝P(-3－h, 0)

由中点公式：(xO为原点横坐标)

2·xP＝xO＋xB，得xP＝3/2；

∴3/2＝-3－h

h＝-9/2

新抛物线：y＝－x²＋2x－3/2.

本文内容由小畅整理编辑！