1957年高考数学试题(1956年高考数学)

导语：1957年高考数学真题，解方程组，几十年后再看依然经典

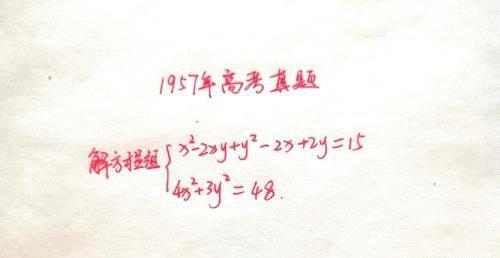
大家好！本文和大家分享一道1957年高考数学真题，这是1957年高考数学副卷的第二题。当年数学副卷共五道大题，其中第一大题包含了5道小题，全卷共9道小题。本题是一道解二元二次方程组的题目，过了六十多年再看这道题依然很经典。

解多元方程组最重要的思路就是消元，本题也不例外。我们先观察一下这两个方程，很明显第二个方程没有太好的处理方法，所以需要从第一个方程入手。

将第一个方程移项后，得到x^2-2xy+y^2-2x+2y-15=0。先对前面的二次三项式进行因式分解，得到(x-y)^2-2(x-y)-15=0，继续分解即可得到(x-y-5)(x-y+3)=0。

不少同学不明白这一步是怎么分解的。其实，用换元法就能够很清晰地展示出这个过程。我们可以令x-y=a，那么原方程就变为了a^2-2a-15=0，此时用十字相乘法就能轻松分解因式了。

当然，也有很多同学说第一个方程可以用双十字相乘法进行因式分解。那么我们先来看一下怎么用双十字相乘法来分解因式。

顾名思义，双十字相乘法就是用了两次十字相乘法，一般用于分解二次六项式。比如分解因式：3x^2+5xy-2y^2+x+9y-4。

第一次十字相乘法：先将3x^2+5xy-2y^2作为一组，用十字相乘法分解得到3x^2+5xy-2y^2=(3x-y)(x+2y)。

第二次十字相乘法：前面三项已经分解成(3x-y)与(x+2y)的积了，然后将-4进行分解，使得交叉相乘的和等于x+9y，即(3x-y)×(-1)+(x+2y)×4=x+9y，所以原式可以分解为(3x-y+4)(x+2y-1)。

另外，应用双十字相乘法分解因式时还可以调整一下分组方法。比如，可以将3x^2+x-4作为一组，先用十字相乘法进行分解，得到3x^2+x-4=(3x-1)(x+4)。在这种情况下，剩下三项的顺序是有要求的，即另外一个平方项只能写在最后一项的位置。这个时候再用第二次十字相乘法进行分解，使得交叉相乘的和等于5xy+9y，即(3x+4)×2y+(x-1)×(-y)=5xy+9y，这样就可以分解出来了。

回到题目。将第一个方程分解后得到的x=y+5或x=y-3。然后再分别代入第二个方程，即可得到两个关于y的一元二次方程。先解出y的值，再求出x的值即可得到原方程组的解。最终，这个方程组算出来有4对实数解。

这是一道很经典的二元二次方程组的题目。对于解多元高次方程组，消元、降幂是基本思路。这道题就分享到这里，你学会了吗？

本文内容由小信整理编辑！