高中物理轻绳类问题有哪些(高中物理轻绳类问题汇总)
导语:高中物理轻绳类问题
理想轻绳,不计质量,也不计发生的微小形变.
一、从力的角度
轻绳弹力沿绳指向绳收缩方向且处处相等.
从效果力看绳子只能提供拉力.
口诀:见绳知方向,见杆要思量,弹簧沿轴向,接触找法向.
1常见受力分析
例题:如图所示,轻绳AD跨过固定在水平横梁BC右端的定滑轮挂住一个质量为10kg的物体,∠ACB=30°,g取10m/s²,求:
(1)轻绳AC段的张力FAC的大小;
(2)横梁BC对C端的支持力的大小及方向.
【受力分析】
2重绳受力分析
例题:如图所示,重为G的链条(均匀的),两端用等长的轻绳连接,挂在等高的地方,绳与水平方向成θ角.试求:
(1)绳子的张力;
(2)链条最低点的张力.
【受力分析图】
重绳具有质量.
3轻绳拉力突变
例题:如图所示,甲、乙、丙为三个完全相同的小球,悬挂在天花板上处于静止状态,甲、乙之间用不可伸长的细线连接,乙、丙之间用轻弹簧连接,某时刻甲上方悬挂在天花板上的细线断开,在细线刚好断开的瞬间,甲、乙、丙三个小球的加速度分别为a1、a2、a3,以下说法正确的是( ).
A a1=g、a2=g、a3=0;
B a1=g、a2=g、a3=g;
C a1=g、a2=2g、a3=0;
D a1=1.5g、a2=1.5g、a3=0
【解析】可用假设法分析,结果只能是甲、乙一起整体下落,即有3mg=2ma,所以a=1.5g.丙瞬间合力仍为0,加速度为0.故选项D正确.
例题:如图所示,一质量为m的小球系于长度分别为L₁、L₂的两根细绳OA、OB上,OB一端悬挂在天花板上,与竖直方向夹角为θ,OA水平拉直,物体处于平衡状态,现在将OA剪断,求剪断瞬间小球的加速度,若将绳OB换为长度为L₂的弹簧,结果又如何?
【解析】无论绳子大小拉力如何,小球所受合力一定不为零,将会运动起来,另一方面小球又受到绳子的约束,因此小球只能做圆周运动.
OA绳断瞬间,小球的瞬时速度为零,因此小球的向心加速度v²/L₁=0,沿绳方向合力为零,绳子拉力为T=mgcosθ,小球的合加速度为a=gsinθ.绳子拉力由mg/cosθ突变为mgcosθ.
☞绳断以后,小球在荡秋千.秋千荡到最高点,往往会误以为加速度为零或者认为是静止状态,其实不是静止,只不过瞬时速度为零,并没有维持速度为零.
例题:质量相同的A、B两小球,用不可伸长的轻绳连接,球A在倾角为θ的光滑轨道内用平行于轨道的轻绳拴在轨道上,球B悬吊在空中,系统静止,如图所示。现将平行于轨道的轻绳剪断,则剪断后的瞬间,A、B两球的加速度大小分别为?
【解析】
这道题是绳子拉力突变问题,也是瞬时加速度问题,还是关联加速度问题.
用关联加速度方法求解比较恰当.绳子的位置还来不及变化,绳子拉力还是在竖直方向上.
绳断瞬间,A球速度为零(速度不会发生突变),B球速度也为零,A、B两球不涉及转动.绳子两端沿绳方向加速度相等.
4活结和死结
①活结的结点可随绳移动,实际上是同一根绳,两段绳子弹力大小一定相等.
例题:如图所示,将一细绳的两端固定于两竖直墙的A、B两点,通过一个光滑的挂钩将某重物挂在绳上,下面给出的四幅图中有可能使物体处于平衡状态的是(C)
【解析】由于重物是通过一个光滑的挂钩挂在绳上,属于活结,绳子拉力处处相等,而两边绳子拉力的合力大小等于重物的重力,方向竖直向上,由对称性可知两边绳子与竖直方向的夹角相等,所以C正确。
例题:如图所示,轻质不可伸长的晾衣绳两端分别固定在竖直杆M、N上的a、b两点,悬挂衣服的衣架钩是光滑的,挂于绳上处于静止状态。如果只人为改变一个条件,当衣架静止时,下列说法正确的是()
A.绳的右端上移到b′,绳子拉力不变
B.将杆N向右移一些,绳子拉力变大
C.绳的两端高度差越小,绳子拉力越小
D.若换挂质量更大的衣服,则衣服架悬挂点右移
②绳子的结点不可随绳移动,是两段独立的绳子,两段绳子弹力大小不一定相等.
例题:如图所示,AO和BO悬挂一个重物,现将绳子AO由如图所示的位置移到竖直,该过程中,OB绳子始终保持水平,则下列说法中正确的是()
A.OA绳子拉力减小
B.OA绳子拉力先减小后增大
C.OB绳子拉力减小
D.OB绳子拉力增大
【解析】
这个结是死结还是活结呢?题目并没有直接说明,因此必须加以推导,如果是活结的话,O点不可能平衡,那就是死结.
用图解法如图所示.
例题:如图甲所示,轻杆OB可绕B点自由转动,另一端O点用细绳OA拉住,固定在左侧墙壁上,质量为M的重物用细绳OC悬挂在轻杆上的O点,OA与轻杆的夹角∠BOA=30°,轻杆OB水平。图乙中水平轻杆OB一端固定在竖直墙壁上,另一端O装有小滑轮,用一根细绳跨过滑轮后悬挂一质量为M的重物,图中∠BOA=30°,则:
(1)图甲、乙中细绳OA的拉力各是多大?
(2)图甲中轻杆受到的弹力是多大?
(3)图乙中轻杆对滑轮的作用力是多大?
5根据绳子位置判断物体状态
例题:在倾角为θ的斜面上,两物体沿斜面相对静止下滑,根据绳子的位置情况,求两物体的加速度.
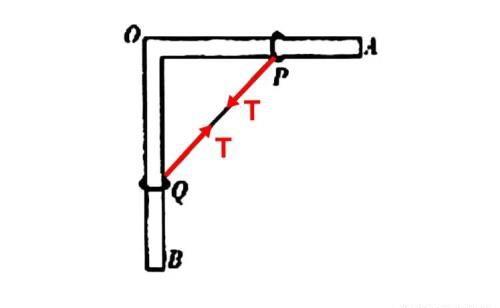
例题:水平放置的固定的光滑硬杆OA,OB成θ角,在两杆上分别套以轻环P,Q,并用轻绳连接两环,现用恒力F沿OB方向拉环Q,当两环达稳定时绳子的张力是多少?
【最后状态受力分析】
二、从运动的角度
1关联速度
由于理想轻绳不可伸长,绳子两端沿绳方向分速度大小相等,方向相同.
2关联加速度
①轻绳两端在同一直线上运动(平动,不涉及转动),两端加速度相等.
例题:如图所示,质量分别为m₁和₂的两个小物块用轻绳连接,绳跨过位于倾角为θ=30°的光滑斜面顶端的轻滑轮,滑轮与转轴之间的摩擦不计,斜面固定在水平桌面上.
【解析】两段绳子的两端没有涉及转动,因此两物体的加速度大小是相等的.
例题:在光滑水平面上,有一质量m₁=20kg的小车,通过一根几乎不可伸长的轻绳与另一质量m₂=25kg的拖车连接。一质量m₃=15kg的物体放在拖车的平板上,物体与平板间的动摩擦因数μ=0.2。开始时,拖车静止,绳未拉紧,如图所示。小车以v₀=3m/s的速度前进。求:
(1)m₁、m₂、m₃以同一速度前进时,其速度的大小。
(2)物体在拖车平板上移动的距离。
【解析】绳子绷紧时候,前后车速度一样.
②轻绳两端不在同一直线上运动(涉及转动),两端加速度不相等.
例题:车和船的加速度关系
【解析】OA段绳子两端涉及转动,加速度是不一样的.
三、从能量角度
由于理想轻绳不可储存能量,轻绳对两端物体做功和为零,对一端物体可以做正功,也可以做负功,也可以不做功.
绳子绷紧瞬间,系统机械能会有损失,转化为内能.
例题:如图甲所示,把系在轻绳上的A、B两球由图示位置同时由静止释放(绳开始时拉直),则在两球向左下摆动时,下列说法中正确的是(CD)
A.绳OA对A球做正功
B.绳AB对B球不做功
C.绳AB对A球做负功
D.绳AB对B球做正功
【解析】用单摆知识判断,A、B两小球哪个在前哪个在后.
例题:长为L的轻绳一端系于固定点O,另一端系质量为m的小球.将小球从O点正下方L/4处,以一定初速度水平向右抛出,经一定时间绳被拉直以后,小球将以O为支点在竖直面内摆动.已知绳刚被拉直时,绳与竖直线成60°角,如图所示.求:
(1)小球水平抛出时的初速度v₀;
(2)在绳被拉直的瞬间,支点O受到的冲量I;
(3)小球摆到最低点时,绳所受拉力Fᴛ.
例题:如图所示,质量m=1kg的小球,通过长l=0.8m的细线悬于O点,平衡时,小球静止于C点,细线不可伸长,质量不计,若将小球拉至使细线成水平状态的A处,然后静止释放,空气阻力不计,试求:
(1)小球运动到C时,细线的拉力;
(2)若把小球拉到与水平面成30°角的位置B处,由静止释放,当小球运动到C时,细线对小球的拉力.
本文内容由小春整理编辑!