利用轴对称求小值的所有情况(如何利用对称轴求小值)

导语：中考专题：利用轴对称性质求最小值

从“利用轴对称性质求最小值”问题入手，挖掘课本资源、注重多题一解、培养知识迁移能力，以此来抛砖引玉，希望同学们认真思考。

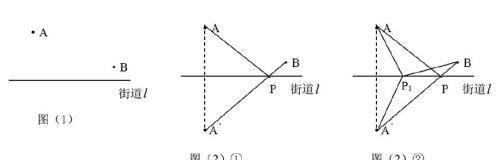
（一）、课本原型：（七年级下册）如图（1）所示，要在街道旁修建一个奶站，向居民区A、B提供牛奶，奶站应建在什么地方，才能使从A，B到它的距离之和最短？

解：如图（2）①，只要画出A点关于直线L的对称点C，连结BC交直线L于P，则P点就是所求。这时PA+PB=PC+PB为最小，（因为两点之间线段最短）。

（证明：如图（2）②，在L上任取一点P1，连结P1A，P1B，P1C，因为P1A+P1B=P1C+P1B>BC=PA+PB。这是根据三角形两边之和大于第三边，所以结论成立。）

（二）应用和延伸：例1、（七年级作业本题）如图（3），∠AOB内有一点P，在OA和OB边上分别找出M、N，使ΔPMN的周长最小。

：如图（4），只要画出P点关于OB、OA的对称点P1，P2 ，连结P1、P2交OB、OA于M、N，此时ΔPMN的周长PM+PN+MN=P1P2为最小。（证明略）

（三）、迁移和拓展：

例1、如图（5），在菱形ABCD中，AB=4a,E在BC上，EC=2a，∠BAD=1200,点P在BD上，则PE+PC的最小值是（ ）

（A）6a (B)5a (C)4a (D)2a

例2、如图（7），在直角坐标系XOY中，X轴上的动点M（X，0）到定点P（5，5）和到Q（2，1）的距离分别为MP和MQ，那么当MP+MQ取最小值时，点M的横坐标X=( )。

（四）、思考与练习：

1、如图（10），∠AOB=450，角内有一点P，PO=10，在角两边上有两点Q、R（均不同于点O），则△PQR的周长最小值是( )。

（提示：画点P关于OA的对称点P1，点P关于OB的对称点P2，∵ ∠AOB=450，∴ΔP1OP2是等腰直角三角形）。又问当ΔPQR周长最小时，∠QPR的度数=( )。

2、如图（14），正方形ABCD的边长为3，E在BC上，且BE=2，P在BD上，求PE+PC的最小值。（与知识拓展例1类似，因为点C和点A关于直线BD对称，所以AE是PC+PE的最小值）。

本文内容由小竹整理编辑！