初中数学翻折问题(重庆中考数学翻折问题)

导语：中考数学压轴题双经典：翻折经典问题，和分类讨论法经典应用

这是中考数学压轴题一道翻折的经典部题，更是运用分类讨论法解决问题的经典题型中的经典。学会解这种题，对中考数学意义非常重大。题目是这样的：

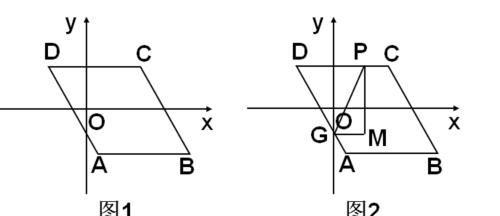
如图1,□ABCD，AB//x轴，AB=6，点A的坐标为(1,-4)，点D的坐标为(-3,4),点B在第四象限，点P是□ABCD边上的一个动点.

(1)假设点P在边BC上，PD=CD，求点P的坐标；

(2)假设点P在边AB，AD上，点P关于坐标轴对称的点Q落在直线y=x-1上，求点P的坐标.

(3)假设点P在边AB，AD，CD上，点G是AD与y轴的交点，如图2，过点P作y轴的平行线PM，过点G作x轴的平行线GM，它们相交于点M，将△PGM沿直线PG翻折，当点M的对应点落在坐标轴上时，求点P的坐标(直接写出答案).

解：易求得B(7,-4), C(3,4),【下面极有可能要运用到这两个点的坐标，因此先把它们求出来。】

(1)当PD=CD时，点P与点C重合，【如果点P不与C点重合，则因为角C是钝角，根据“大角对大边”，就必有PD>CD】

(2)设Q(x,x-1)，则P(x,1-x)或P(-x,x-1), 【前者关于x轴对称，后者关于y轴对称】

直线AD的解析式为：y=(4-(-4))(x-1)/(-3-1)-4=-2x-2,【运用了直线的点斜式y-y0=k(x-x0)，其中(x0,y0)取的是A点的坐标。斜率k=(yc-yA)/(xc-xA)】

当点P在AB上时, 1-x=±4, 解得x=5或x=-3,【注意1-x=4时，x=5对应的是(x,1-x), 1-x=-4时，x=-3，对应的是(-x,x-1)】

当点P在AD上时, 1-x=-2x-2或x-1=2x-2, 解得x=-3或x=1,【同上，要注意对应问题。这里运用分类讨论法，又包含有交叉分类的情况】

∴P(5,-4)或(3,-4)或(-3,4)或(-1,0).

(3)P(6根号5/5, 4)或(-6根号5/5, 4)或(-5/2,3)或P(2,-4).【答案可以直接写出来，分析过程却非常复杂，仍运用分类讨论的方法。分析部分不必写在解题过程中】

分析：(3)由(2)知G(0,-2), 设P(p,y)，则M(p,-2),

当P点在CD上时, P(p,4), (-3≤p≤3)

若M点的对应点在y轴上，则△PMG是等腰直角三角形, 【因为此时对称图形是一个正方形，这是分类中的分类，即分层分类讨论的应用】

MG=PM，即p=(4-(-2))=6>3(舍去).【这种情形不存在】

若M点的对应点M’在x轴上，则设M’(m,0),

MG=M’G, 即|p|=根号(m^2+4),PM=PM’, 6=根号((p-m)^2+16)，【就是对称构成全等三角形，三边相等。全等三角形，有公共边和两个公共顶点，这样就形成关于公共边轴对称的关系】

解得：p=±6根号4/5. 【这个方程组很不好解】

P(6根号4/5, 4)或(-6根号4/5, 4).

当P点在AD上时, P(p,-2p-2), (-3≤p≤1)

易知点M的对应点不在y轴上, 同上有【仍利用全等且对称的特殊关系来分析】

|p|=根号(m^2+4),PM=PM’, |-2p-2-(-2)|=根号((p-m)^2+16)，

解得：p=-5/2,【这个方程组也特别难解】

-2p-2=3, 有P(-5/2,3),

当P点在AB上时, P(p,-4), (1≤p≤7)

△PMG是等腰直角三角形, MG=MP，即p=(-2-(-4))=2.P(2,-4).

题目虽然挺麻烦，但老黄特别喜欢这样的题目。学生的逻辑思维，就是在解这类题目的过程中，慢慢建立起来的。

本文内容由小馨整理编辑！