函数不连续就不能用微积分进行研究吗为什么(函数不连续可以积分吗)

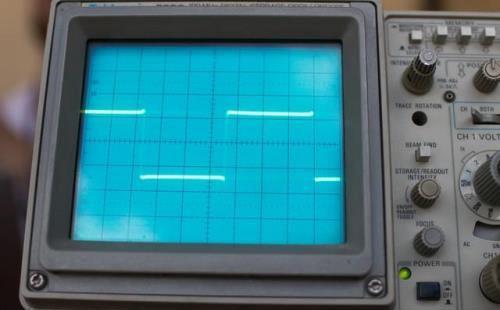
示波器正在检查方波信号

一般的微积分教程，第一章就是 函数，极限，连续。

接着讲导数，再后边讲 拉格朗日 中值定理等。

条件都是 函数在 闭区间内连续，在开区间内可导

那只要函数不连续的点，就不能用微积分进行研究吗？

微积分也是 可以用来研究函数不连续的点的。

典型的，用傅里叶级数合成方波信号

方波信号函数在零点突然跳动，从负一跳动到正一，那这样的波形 可以用 正弦波 和 余弦波 合成吗？

这不止是个理论问题，也是个实际问题。

因为计算傅里叶级数系数 只用到积分，没有用到微分，所以函数不连续点，也可以做傅里叶级数展开。

展开以后级数的和，在这点等于 左极限 和 右极限的平均值。

由什么样的函数 可以进行 傅里叶级数 展开 这个问题，又引发了什么是函数的积分这个问题，实现了 积分的 黎曼定义 到 勒贝格 积分定义的发展。

这不是玄学讨论，正余弦波的合成结果，可以用示波器实实在在看。

数学理论的发展 也是受 实际应用的激发 而产生的，不是凭空想象出来的。

类似于 瓦特 刚发明 蒸汽机的时代，没有人讨论 发动机 是不是必须有活塞这样的 问题。

因为 当时 各种机械 都需要将 动力输出为 旋转运动，所以发动机都是有活塞的。

等飞机刚发明以后，人们依然在飞机上采用活塞式发动机。

但是飞机飞行，不需要有轮子，只要有向后的推力就可以了。

所以以前发动机上，用于把往复运动转化为旋转运动的一套机制，在飞机上其实没有必要。

就有人想到了 把 活塞式发动机驱动螺旋桨 的飞机 更换为 喷气发动机，把冗余的活塞去掉。

这样提高了能量转化效率，极大的提高了飞机的飞行速度。

这时候，讨论发动机是否必须有活塞，什么情景下需要活塞就有意义了。

那喷气发动机 发明以前的 发动机教科书，第一章 一定不会给 发动机分类，分成活塞式和非活塞式。

现在 好多微积分 教材，第一章 讲函数，极限，连续，又给 间断点 做了分类，分成第一类间断点 和 第二类 间断点。

就是类似 喷气式 发动机发明以后，发动机教科书 第一章 给发动机 分类。

问题在于，喷气发动机人们在日常生活中，已经见过，所以讨论这个分类，学生觉得正常，一点也不觉得玄。

而傅里叶级数展开，刚学微积分的人，是没有直觉上的理解的，这时候 给 间断点 分类，相当于只说了 半句话，让学生觉得数学研究的内容有些玄，脱离实际。

类似于小学生 识字 有些意思复杂的字，只能从应用环境中理解意思。

但是 归类识字 又是按 偏旁部首 识字。

所以 在学生 不知道这个字的意思的前提下，

让学生反复练习这个字如何写，分析这个字是什么偏旁，这个字有几划，笔顺应该是如何。

这大大影响了学生的学习兴趣。

数学理论也是受实际的应用场景的需要而发展出来的，一般都是先有问题，再发展出计算方法，最后才严密化，这个过程长的有几百年。

牛顿刚发明 微积分时，用无穷小来说明问题。

一百多年以后，柯西提出现在 教材中广泛使用的 极限概念。

又过了一百多年，黎曼提出了 现在教材中 广泛 采用的 积分的 黎曼定义。

数学家黎曼

数学本来 是 为了解决 实际问题而发展出来的，是先有问题，后有理论。

所以学习数学，也应该从实际应用中学，让学生从 实际问题 到 解决问题 的 理论发展 这个完整的过程。 通过这个过程，学生不止学到了数学知识，而且发展出了创造能力。

这个过程相当于 从 课文中学汉字，先知道意思，再熟悉如何写。

一些数学教材的编写思路，类似于按偏旁部首识字的思维，不讲字的意思，按偏旁部首，让学生反复练习 笔画，笔顺，字体结构 。有可能学生把这个字都写吐了，还不知道具体是什么意思，在什么环境下使用。

繁体的书字

典型的 高中的 数列 是 为了 给以后学习级数做准备的，但是很少讲级数的应用场景，把主要精力放在各种技巧的练习上。

有好多人，选的专业，以后的课程不学级数。

这就相当于 一个字 写了 几百遍，分析了字的结构，笔顺，笔画 部首 等等，以后在实际读写中从来没有使用过这个字。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小春创作整理编辑！