函数的图像及其变换归纳总结怎么写(函数的图像及其变换归纳总结图)

导语：函数的图像及其变换归纳总结

一、课标要求：

函数是现代数学中最基本的概念，是描述客观世界中变量关系和规律的最为基本的数学语言和工具，在解决实际问题汇总发挥重要作用。函数是贯穿高中数学课程的主线。

1．函数概念与性质

本单元的学习，可以帮助学生建立完整的函数概念，不仅把函数理解为刻画变量之间依赖关系的数学语言和工具，也把函数理解为实数集合之间的对应关系；能用代数运算和函数图象揭示函数的主要性质；在现实问题中，能利用函数构建模型，解决问题。

（1）函数概念

①在初中用变量之间的依赖关系描述函数的基础上，用集合语言和对应关系刻画函数，建立完整的函数概念（参见案例2），体会集合语言和对应关系在刻画函数概念中的作用。了解构成函数的要素，能求简单函数的定义域。

②在实际情境中，会根据不同的需要选择恰当的方法（如图象法、列表法、解析法）表示函数，理解函数图象的作用。

③通过具体实例，了解简单的分段函数，并能简单应用。

（2）函数性质

①借助函数图象，会用符号语言表达函数的单调性、最大值、最小值，理解它们的作用和实际意义。

②结合具体函数，了解奇偶性的概念和几何意义。

③结合三角函数，了解周期性的概念和几何意义。

2．幂函数、指数函数、对数函数

幂函数、指数函数与对数函数是最基本的、应用最广泛的函数，是进一步研究数学的基础。本单元的学习，可以帮助学生学会用函数图象和代数运算的方法研究这些函数的性质；理解这些函数中所蕴含的运算规律；运用这些函数建立模型，解决简单的实际问题，体会这些函数在解决实际问题中的作用。

内容包括：幂函数、指数函数、对数函数。

（1）幂函数

（2）指数函数

（3)对数函数

二、知识梳理

1.图像的变换

（1） 两个函数图象间的变换及函数关系：【会根据变换写解析式】

平移变换：

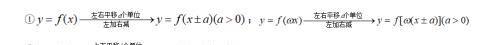
（2）翻折变换：

（3）伸缩变换：

（4） (对称变换)两个函数图象间的对称性及函数关系：【会根据对称性写解析式】

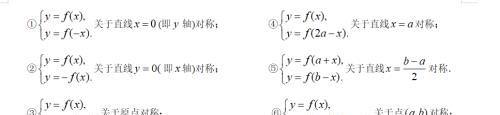
2.函数图像的应用

（1）.利用函数图像确定函数解析式

利用函数图像确定函数解析式时,要注意综合应用奇偶性、单调性等相关性质，同时结合自变量与函数值的对应关系.

（2）利用函数图像研究两函数图像交点的个数

利用函数图像研究两函数图像交点的个数时,常将两函数图像在同一坐标系内作出,利用数形结合求解参数的取值范围.

（3）利用函数图像研究不等式

当不等式问题不能用代数法求解但其与函数有关时,常将不等式问题转化为两函数图像的上、下关系问题,从而利用数形结合求解.

（4）利用函数图像研究方程根的个数

【会读图】读出定义域，值域，最值，极值，零点，解集，单调性，奇偶性（对称性），周期性，有界性，渐近线．

【会作图】熟练掌握一些基本函数图象．作图时，抓住关键点（端点、最值点、极值点、零点、与y轴的交点、对称中心等），关键线（对称轴、渐近线），利用好函数性质（奇偶性、单调性、周期性等）．

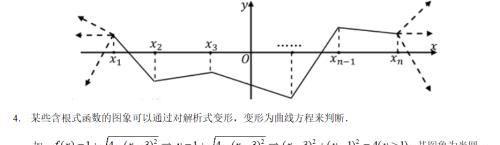
三、查缺补漏

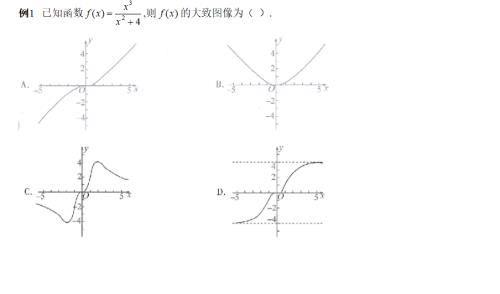
1.识图，辩图

（1）从函数的定义域,判断图像左右的位置；

（2）从函数的值域,判断图像的上下位置；

（3）从函数的单调性,判断图像的变化趋势；

（4）从函数的奇偶性,判断图像的对称性；

（5）从函数的周期性,判断图像的循环往复.

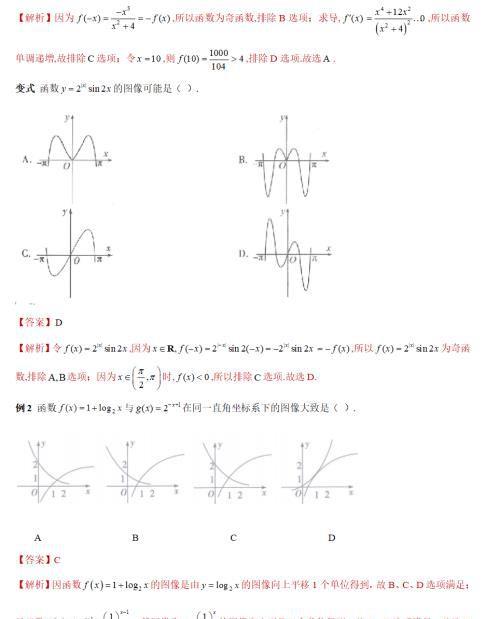
2.图像的变换

3.图像的应用

四、常用二级结论：

1.函数图像对称性

2. 二次函数

3.经典不等式．

三年真题：

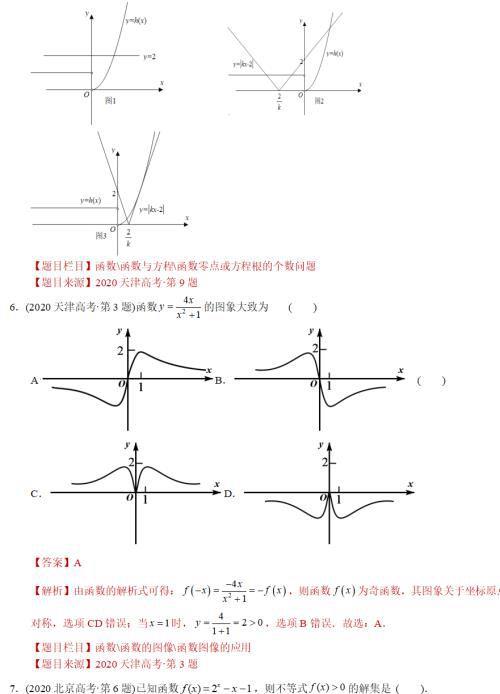
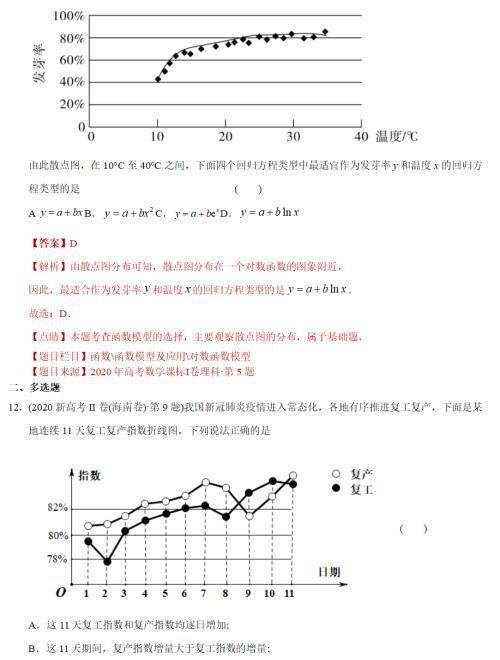
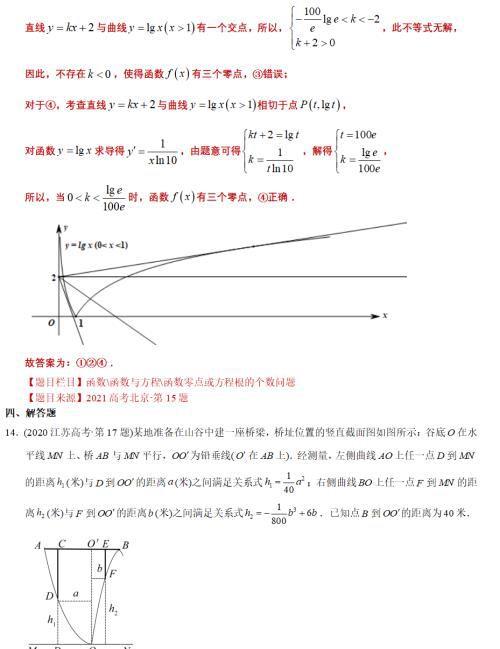
免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小婷创作整理编辑！