基本图形中的等腰三角形(等腰三角形的作图方法)

导语：基本图形分析法：等腰三角形（一）

当几何问题中出现了两条具有公共端点且不在一直线上的相等线段时，无论它们是在条件中出现还是在结论中出现，就应萌发应用等腰三角形的基本图形进行证明的意识。然后就应将这两条具有公共端点的相等线段组成等腰三角形，如果图形中尚未出底边的，就应将底边添上。接下来就应应用等腰三角形中两条边相等和相对应的两个角相等之间的等价关系，将要证明的结论转化为要证明它的等价性质，或者由条件直接推得它的等价性质成立。若图形中出现了等腰三角形顶角的外角时，则应将两内角之间的相等关系转化为等价的外角与不相邻的内角之间的倍半关系来进行证明。

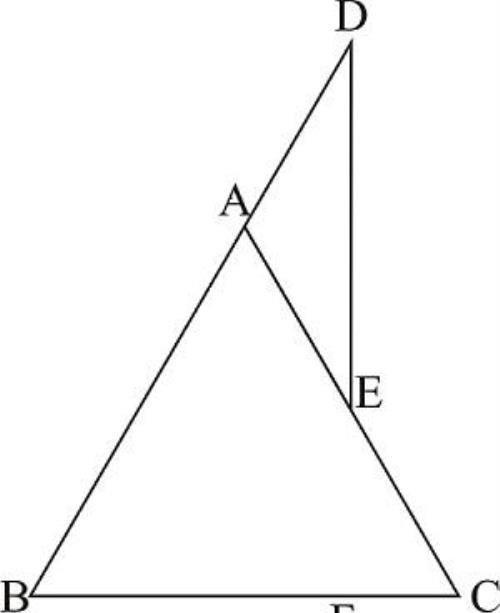
例1如图 3-1，已知：△ABC中，AB=AC，E是AC上的一点，D是BA的延长线上的一点且AD=AE，求证：DE⊥BC。

图3-1

分析：本题要证明的结论是DE⊥BC，这是证明两条线段垂直的问题，根据垂线的定义它们应相交成90°角，而现在它们尚未相交，所以应将它们延长到相交，也就是延长DE交BC于F（如图3-2），问题就成为要证∠DFB（或∠EFC）=90°。由于∠DFB可以看作是△DFB的一个内角，所以要证明这个角是直角，也就是要证明这个三角形中另外两个角的和等于90°，也即要证∠D+∠B=90°。

图3-2

由条件中出现AB=AC是两条具有公共端点的相等线段，所以它们可组成一个等腰三角形，从而可应用等腰三角形的基本图形的性质进行证明。又因为B、A、D成一直线，出现了这等腰三角形的顶角的外角，所以可得∠DAE=2∠B。又因为条件中还出现AD=AE，也是两条具有公共端点的相等线段，它们也可以组成等腰△ADE，而由D、A、B成一直线，又可得∠BAC=2∠D。而∠DAE+∠BAC=180°，所以∠D+∠B=90°就可以证明。

例2 如图3-3，已知：AB是⊙O的弦，延长AB到C，使BC=BO，直线CO交⊙O于D、E。求证：弧AB=3×弧BD。

图3-3

分析：本题要证明的结论是两条弧之间的倍数关系，或者讲是两条弧之间的一种数量关系。在几何问题的分析中，对于弧之间的数量关系的基本的处理方法就是转化成为与圆有关的角之间的数量关系来进行讨论。

由于在图形中对于弧BD来说，它所对的圆心角∠BOD已经出现，所以对弧AE来说也需要用它所对的圆心角，但这个圆心角现在图形中尚未出现，所以根据圆心角的定义，可联结OA（如图3-4），则∠AOE就是弧AE所对的圆心角，那么问题即可转化为要证∠AOE=3∠BOD。

图3-4

由条件BC=BO，这是两条具有公共端点B的相等线段，它们可以组成一个等腰三角形，所以就可应用等腰三角形的基本图形的性质进行证明。根据条件C、B、A成一直线，这就出现了∠ABO是等腰△BCO的顶角的外角，从而就有∠ABO=2∠BOD=2∠C。又因为OA和OB是同圆的两条半径，当然相等，所以它们也是两条具有公共端点的相等线段，也就可以组成等腰三角形，应用等腰三角形这个基本图形的性质又可以得∠A=∠ABO。

由于条件中还给出C、O、E成一直线，这样结论中出现的∠AOE就可以看作是△OAC的一个外角，从而有∠AOE=∠A+∠C=2∠BOD+∠BOD，分析就可以完成。

本文内容由小芦整理编辑！