三角形中线用法(三角形中线简便公式)
导语:三角形中线的巧用
结论一:三角形的一边的中线把这个三角形分成面积相等的两部分。
结论二:连接三角形的中线的交点和这个三角形任意两个顶点所组成的三角形的面积等于这个三角形面积的.
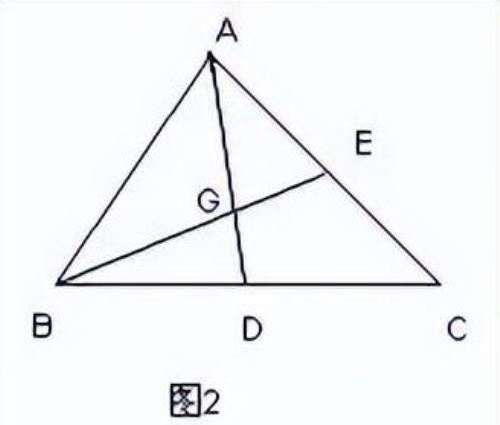
析解:因为AD.BE是△ABC的两条中线,根据结论一,三角形ADC的面积等于三角形ABC的面积的一半,三角形BCE的面积也等于三角形ABC的面积的一半。
如图3,由结论一可知S△BGD=S△CDG,S△CEG=S△AEG,S△ACD=S△BCE=
用△ACD与△BCE的面积同时减掉四边形CDGE的面积可得S△BGD=S△AGE,所以,
,所以
例题1:有一块三角形优良品种试验基地,如图所示,由于引进四个优良品种进行对比试验,需将这块土地分成面积相等的四块,请你制定出两种以上的划分方案供选择.(画图说明)
解:方案1:如答图 (1),在BC上取D、E、F,使BD=ED=EF=FC,连接AE、AD、 AF.
方案2:如答图 (2),分别取AB、BC、CA的中点D、E、F,连接DE、EF、DF.
方案3:如答图 (3),分别取BC的中点D,CD的中点E,AB的中点F,连接AD、AE、DF.
点拨:可根据中线所分的两个三角形的面积相等以及三角形的面积公式的特征,先分为两个面积相等的三角形,然后再依次等分.
例题2: 已知:如图3,△ABC中,M是AB中点,MD⊥BC,EC⊥BC,S△ABC=24,求S△BDE.
解:连接MC,由题意知:DM∥EC,∴S△DME=S△DMC,又∵M为AB中点,
∴S△BCM=1/2S△ABC,∴S△BDE=S△BCM=1/2S△ABC=12.
例题3:如图3-1,正方形ABCD的 边长为1,E.F分别是AB.BC边上的中点,求图中阴影部分的面积。
分析:图中阴影部分是不规则四边形,须作辅助线转化为规则四边形或三角形。更重要的是要考虑中点的运用。
解:如图3-2,连接BD,则三角形BCD的面积=
根据上述结论二,△ BOD的面积等于△BCD的面积的1/3,
即
,
∴阴影部分的面积=
.
点评:求不规则图形的面积往往是作辅助线转化为三角形加以分析,记住上面的两个结论,能够迅速巧妙的求解此题。
本文内容由小萱整理编辑!