清宫定理证明方法(清宫定理是几年级学的)

导语：清宫定理证明

清宫定理是日本数学家清宫俊雄提出的，并以他的名字命名。

清宫定理：一个三角形的外接圆上有两点（不与三角形的顶点重合），其中第二点与第一点关于各边对称的点的连线与对应的各边或其延长线相交，则三个交点共线。

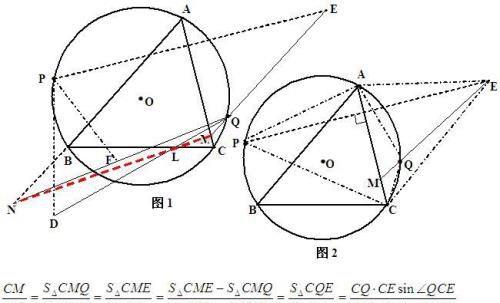
如图1，设P、Q为△ABC的外接圆上异于A、B、C的两点，P关于三边BC、CA、AB的对称点分别是D、E、F，且QD交BC于L，QE交AC于M，QF交AB的延长线于N，则L、M、N三点在同一直线上。

分析：此定理的证明，可以用梅涅劳斯定理来证明，把MLN作梅氏直线，则要证（CM/MA）×（AN/BN）×（BL/LC）＝1，这就要转化CM/MA，AN/BN，BL/LC。可用CQ，CP，AQ，AP，BQ，BP及相应的角的正弦值来表示它们。

如图2，连结AP，AQ，AE，CP，CQ，CE

∵CA垂直平分PE，∴CE＝CP，∠ACE＝∠ACP，∵∠QCE＝ACE－∠ACQ，

∴∠QCE＝∠ACP－∠ACQ；

又AE＝AP，∠CAE＝∠CAP，∠QAE＝∠CAE－∠CAQ，∴∠QAE＝∠CAP－∠CAQ，∴

下面我们再来转化AN∶NB，本来可以用同理可证直接写出表达式，但考虑到是和读者交流，为把问题分析得更清楚，笔者不用同理转化AN∶NB和BL∶LC。

如图3，连结AP，AQ，AF，BP，BQ，BF

∵AB垂直平分PF，∴AF＝AP，∠BAF＝∠BAP，∵∠QAF＝∠BAQ－∠BAF，

∴∠QAF＝∠BAQ－∠BAP；

又BF＝BP，∠ABF＝∠ABP，∠QBF＝∠ABF－∠ABQ，∴∠QBF＝∠ABP－∠ABQ

如图4，连结BP，BQ，BD，CP，CQ，CD

∵CB垂直平分PD，∴BD＝BP，∠CBD＝∠CBP，∵∠QBD＝∠CBD＋∠CBQ，

∴∠QBD＝∠CBP＋∠CBQ；

又CD＝CP，∠BCD＝∠BCP，∠QCD＝∠BCD＋∠BCQ，∴∠QCD＝∠BCP＋∠BCQ

如图5，∵∠ACP＝∠ABP，∠ACQ＝∠ABQ，∴∠ACP－∠ACQ=∠ABP－∠ABQ

∴sin（∠ACP－∠ACQ）＝sin（∠ABP－∠ABQ）

又（∠CBQ＋∠CBP）＋（∠CAP－∠CAQ）＝（∠CBP＋∠CAP）＋（∠CBQ－∠CAQ）

∵∠CBP＋∠CAP＝180º，∠CBQ＝∠CAQ，

∴（∠CBQ＋∠CBP）＋（∠CAP－∠CAQ）＝180º

∴sin（∠CBQ＋∠CBP）＝ sin（∠CAP－∠CAQ）

同理：sin（∠BCQ＋∠BCP）＝ sin（∠BAQ－∠BAP），∴

由梅涅劳斯定理定理得：L、M、N三点共线。

本文内容由小蔼整理编辑！