圆辅助线口诀(圆常用辅助线模型)

导语：中考几何进阶 31 辅助线法则 圆幂的概念和圆幂定理

中考几何进阶 31 辅助线法则 圆幂的概念和圆幂定理

【圆幂的定义】

对于一个已知圆，和一个不在圆上的已知点P，该点到该圆的最小距离与最大距离的乘积的绝对值，称为该点对该圆的圆幂，简称点P的圆幂。

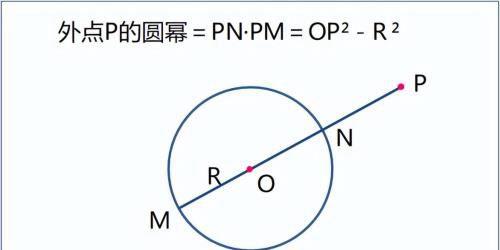
P在圆外：

P在园内：

【圆幂定理】

之所以有上述圆幂定义，乃因为如下事实：

过P引任意一条与圆相交或相切的直线，设与圆相交于点A和点B（A、B可重合因而成切线），则PA·PB的值等于圆幂，是一个定值。

这个结论，便称之为圆幂定理。

【割线定理】

当P在圆外，圆幂定理又称为割线定理，并表述为：

过P的任意两条直线L1和L2，分别与圆相交于A、B和C、D，则

PA·PB＝PC·PD

【切割线定理】

若其中的C、D重合，并记为点T，则L2为圆的一条切线，则

PT²＝PA·PB

此时亦称为切割线定理。

【相交弦定理】

若P点在圆内，圆幂定理又称为相交弦定理，表述为：

过P的两条弦分别交圆于A、B和C、D，则

PA·PB＝PC·PD

通过相似三角形，可以证明以上诸定理。在此略过。

圆幂定理的几何图像，如所示。

这里把弦切角定理，也归纳入圆幂定理当中。

圆幂定理的逆应用，提供了另外判断四点共圆的方法：若PA·PB＝PC·PD，则A、B、C、D四点共圆。

应用题例

如图△ABC和Rt△AED，E是BC上一点，且BE＝11，CE＝3；AB＝AC＝AD，求ED的长度？

〖一般性提点〗

求线段长度或者线段比，通常是求解Rt三角形，或者通过全等三角形，或者相似三角形等方法来找未知线段和已知线段之间的关系。

如何去构造这些三角形，则具体问题要具体分析。

〖题目分析〗

解Rt三角形或者找全等三角形求未知线段，从题设看不到任何思路。余下的途径就是寻找或构造相似三角形。

题设已知条件，有共点的诸相等线段。我们知道到一个定点的距离相等的诸点共圆，而且已知线段BEC会让人想起相交弦定理：BC是圆的一条弦，而所求ED是另一条弦的部分。

B、C、D均在以A为圆心，以AB为半径的圆上，延长DE交圆A于另一点F，根据垂径定理：EF＝ED。连接CD、BF，则△CDE∽△FBE，或者直接由相交弦定理，有：

ED·EF＝BE·CE，即

ED²＝BE·CE＝33

ED＝√33.

本文内容由小姿整理编辑！