三角形中线的特点是什么(三角形中线有什么特点)

导语：三角形中线的一个特点

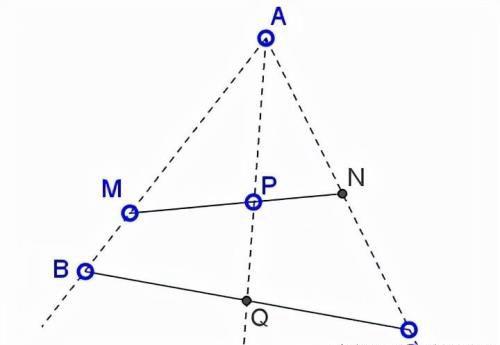
在ΔABC中，Q是BC的中点;P是AQ上的一点，通过P的直线与AB相交M点，与AC相交于N点。证明BM/MA+CN/NA与线段MN无关，只与点P有关。

证法1：通过B点和C点分别做中线QA的平行线，与MN交于D点和F点。

由于两对相似三角形的存在有：

由于四边形BCFD是梯形， PQ是中线，所以:

因此有：

这个数十个常数，不管线段MN怎么变化，只和P点有关。

当P是三角形的形心时候，这个常数是1.

证法2：如图过B点和Q点做MN的平行线，交于AC于V，W点，

设线段AP=m, PS=n, SQ=t.

AN=z, NV=y, VW=WC=x (因为Q是中点，则W是VC的中点)

根据多个相似的三角形有：

BM/MA=n/m

n/t=y/x, 即y=nx/t

m/n=z/y, 即z=my/n=mx/t

因此：

CN/NA=(2x+y)/z=(2t+n)/m

所以：

BM/MA+CN/NA=(2n+2t)/m=2(n+t)/m=2PQ/PA

即只与P点的位置有关。

本文内容由小凡整理编辑！