求阴影面积如图所示(求阴影面积603020)

导语：求阴影面积：BE=EC，S△AGD=18，S△ABG=20，S△GCD=45，求S▲AED

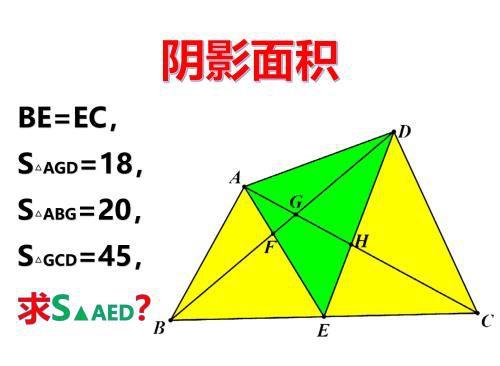
题目：如图：BE=EC，S△AGD=18，S△ABG=20，S△GCD=45，求S▲AED？

分析：这是一道基本的平面几何题目，涉及到中点、三角形面积计算等基本概念和公式。难度适中，适合小学或者初中阶段的学生练习。需要考生对所学知识点有一定理解和应用能力。整道题目看似普通，但在解题过程中也有些许乘除法的思想在其中，培养了学生扎实的数学运算能力。同时，这道题目也有教育意义，不仅能让学生更好地理解中点的概念，还能培养学生的数据分析和解决问题的能力。

解法1：S△BCG=45×20/18=50，S总=133，S△CDE=½×(50+45)=47.5，S△ABE=½×(50+20)=35，S▲AED=133-47.5-35=50.5。

小结：这个解法计算过程简单明了，使用了基本的面积计算公式，步骤清晰，容易理解。同时，也充分体现了数学知识的应用和实际问题的解决能力。整个计算过程中没有使用过复杂的数学工具或技巧，是一种简单而实用的计算方法。不仅考察了学生的计算能力，也培养了学生的数据分析能力和解决问题的能力。值得一提的是该解法的最后一步独特而巧妙，通过减法求得了最终的结果，易于理解和掌握。因此，这种解法也有一定的启发意义，能够帮助学生更好地理解三角形面积计算的方法和技巧，拓展学生的解题思路。

解法2：①BG:DG=S△ABG:S△ADG=10:9，②BG:DG=S△BGC:S△DGC，即10:9=S△BGC:45，得S△BGC=50，则SABCD=20+18+45+50=133，③己知E为BC的中点，则S△DCE=S△DBE=S△DBC/2=(45＋50)/2=47.5，S△ABE=S△ACE=S△ABC/2=(20+50)/2=37.5④所求S▲AED=SABCD-S△DCE-S△ABE=133-47.5-35=50.5。

小结：这个解法通过比例分析了三角形AGD和ABG的面积比例，使用了对应边的比例关系，并与三角形BGC和DGC的面积比例进行了对比，找到了正确的比例系数。然后通过面积计算公式，计算出四边形ABCD的面积。在求解三角形AED面积时，使用了中点的性质，以两个三角形的面积为基础进行面积的综合计算，计算过程简单而逻辑清晰。这种解法在理论上比较严谨，使用了比例和面积的变形运算，考验了学生的思维能力和数学综合运用能力。不同于解法1，该解法更加注重了基础知识的灵活运用和逻辑思维的拓展，有一定的难度，适合有一定基础的学生练习。

解法3：三角形ADB和ADC，面积为38和63，两三角形为同底，可以求出两个三角形高的比值，E为BC的中点，三角形ADE的高EK为两高a、b和的一半 ，故可求出S▲AED=(38+63)/2=50.5。

小结：这个解法同样是正确的。它采用了几何图形的对称性原理，通过比较三角形ADB和ADC的面积，得到两个三角形的高的比值，然后根据三角形的高的性质，推导出了三角形AED的面积。由于使用了几何图形的对称性原理，计算方法简单，基本不需要直接计算面积，避免了复杂的计算步骤，因此更加简便。然而，该解法需要学生对对称性原理有一定的理解和运用能力，并且需要对几何图形有一定的分析能力。相对于解法1和解法2，该解法没有直接使用面积的计算公式，更加注重了几何图形的特性和原理，更具有启发性和挑战性。总之，这种解题方式能够帮助学生加深对几何知识的理解，提高学生的几何思维能力。

总结：这道题目可以通过多种解法来获得答案，做题者可以根据自己的知识水平和思维习惯，选择不同的解题方法进行计算。解法一采用面积计算公式，比较直接；解法二采用了对应边的比例关系，依赖比例推导；解法三则利用了几何图形的对称性原理，减少了计算的步骤。每种解法都有其优点和适用条件，但不同方法之间的计算复杂性难以判断。综上所述，多样化的解法为学生提供了更多的思考角度和解题方法，可以更好地帮助学生加深对几何知识的理解和运用，提高他们的解决问题的能力。

如有其它解题思路欢迎评论区分享。

本文内容由小春整理编辑！