二次函数是中考的重点、热点，可与多个知识点相结合，本篇主要简单介绍下二次函数中几何图形线段、周长、面积最值问题。线段最值一般的处理思路有：（1）利用点的坐标，通过距离公式表示出线段的长度，然后通过研究二次函数的性质得到线段最值；（2）将未知的线段通过相似三角形或锐角三角函数转化为可求的线段，然后再通过二次函数进行研究。周长最值问题情况较多，可能是通过几何最值模型进行转化，比如将军饮马模型、造桥选址模型等，也可能通过相似三角形，转化为线段最值问题，面积最值问题常用的两种处理方式：（1）铅锤法；（2）平移法。

线段最值

例题1：如图，直线y=-x+4交x轴于点A，交y轴于点C，抛物线y＝1/2x^2+bx+c经过点A，交y轴于点B（0，-2），点D为抛物线上一动点，过点D作x轴的垂线，交直线AC于点P，设点D的横坐标为m．

（1）求抛物线的解析式．

（2）当点D在直线AC下方的抛物线上运动时，求出PD长度的最大值．

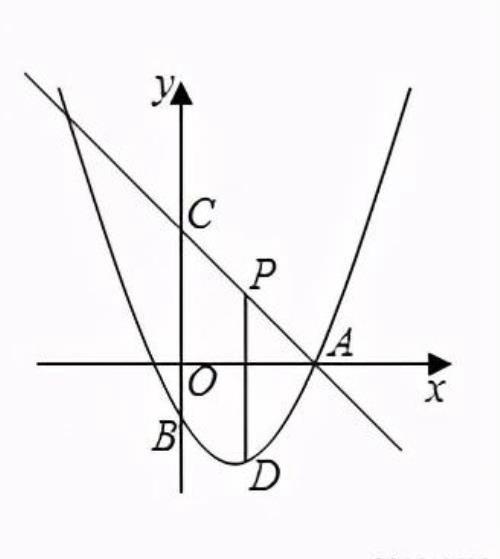
分析：待定系数法求函数解析式，先由直线解析式求出点A坐标，然后通过待定系数法求出二次函数解析式。用含m的代数式表示点P，D的坐标，由点D在直线AC下方的抛物线上，可用含m的代数式表示出PD的长，利用函数的思想和性质可求出线段PD的最大值。

本题直接通过点坐标表示出线段的长度，由于PD∥y轴，那么PD之间的距离，可以通过：上面点的纵坐标减去下面点的纵坐标求出。

周长最值

例题2：如图，抛物线y=a（x-5/2）^2+h经过点A（1，0），C（0，3）．

（1）求抛物线与x轴的另一个交点B的坐标；

（2）如图①，在抛物线的对称轴上是否存在点P，使得四边形PAOC的周长最小？若存在，求出此时P点坐标；若不存在，请说明理由

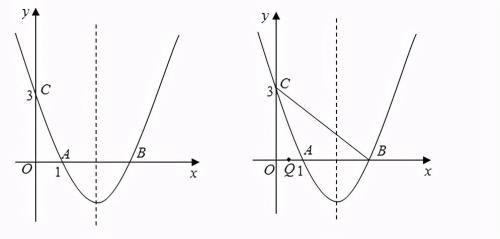
分析：函数解析式是顶点式，已知抛物线的对称轴，通过二次函数的对称性即可求出抛物线与x轴的另一个交点坐标。求四边形PAOC的周长，即求PA+OA+AC+CP四条线段和的最小值，线段OA、OC的长度不变，那么就是求AC+CP的最小值，典型的将军饮马模型，连接BC交对称轴于点P，则P点即为所求。

本题求周长最值问题，将其转化为模型进行求解，难度不大。

面积最值

例题3：如图，抛物线y=-x^2-2x+3与x轴交于A、B两点，与y轴交于点C．

（1）求A、B、C三点的坐标；

（2）在该抛物线的对称轴上是否存在点P，使得△PAC的周长最小？若存在，求出点P的坐标；若不存在，请说明理由；

（3）抛物线上在第二象限内是否存在一点Q，使△QBC的面积最大？若存在，求出点Q的坐标及△QBC的面积最大值；若不存在，请说明理由．

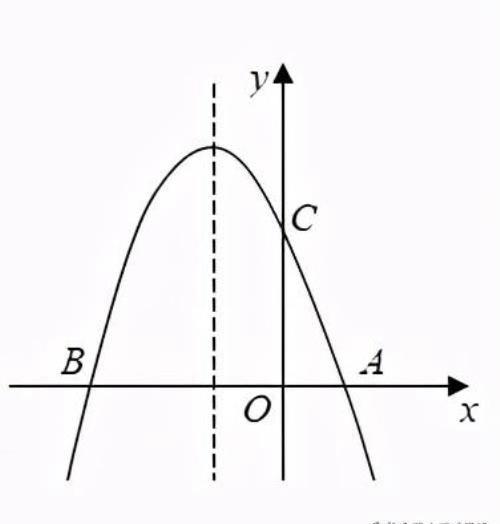
分析：（1）求抛物线与x轴、y轴的交点坐标，可分别令x=0、y=0；

（2）求△PAC周长最小值，即求PA+PC+AC三条线段和的最小值，线段AC的长度不变，那么求PA+PC的最小值，典型的将军饮马模型，根据抛物线的对称性可知，点A关于对称轴的对称点为点B，连接BC与对称轴的交点即为点P。求点P坐标，可以通过求直线解析式或相似三角形；

（3）根据S△QBC=S△QBP+S四边形QPOC-S△BOC即可求得解析式，根据解析式即可求得求出点Q的坐标及△QBC的面积最大值．

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小余创作整理编辑！