初中平面几何难题辅助线(初中数学几何常见辅助线作法口诀)

导语：中考几何进阶 11 辅助线法则（11）一道求面积的几何题

中考几何进阶 11 辅助线法则（11）一道求面积的题

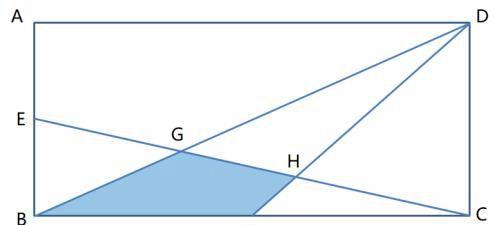
题： 已知长方形ABCD面积是36，E、F分别是AB、BC中点；BD、DF分别交CE于G、H，求阴影面积。

〖分析〗

先把残余的四方形划分成三角形：连接DE、BH。不建议AG和FG，因为图形中有相似三角形，要利用这个条件，因为面积比无非就是和线段比发生事情。各三角形标号如图，便于讲解。

见图，②＋③和⑤这两个三角形相似（∵AB∥CD），相似比k=CD∶EB=2。这个是关键。

由等积模型易知，S(△BDF)＝S(□ABCD)/4＝=9；显然需要求得③号的面积：阴影面积＝S(△BDF)－S(③)。

由平行四边形等积模型，②＋③＋④这个三角形面积是□ABCD的一半：S(②＋③＋④)＝S(□ABCD)/2＝18。这样，或者求出②或④的面积，或者求出它们与③的面积比。

先看④，显然S(④＋⑤)＝S(□ABCD)/4＝9；而且S(④)∶S(⑤)＝k＝2，解得：S(⑤)＝3，S(④)＝6。

接下来就得解决②号的面积问题了。看不出能直接求②号面积的途径，所以寻求②与③号的面积比，这必然要通过“中介”。所谓中介者，既要与②号有关系，又要与③号有关系。

一个明显的中介是⑤号，S(②＋③)∶S(⑤)＝k^2，S(②＋③)＝4 S(⑤)＝12，又拐到要求②号面积，由前分析，此路不通。

另一个可能的中介是①号。在①＋②＋③这个三角形中，由燕尾定理可知：S(①＋③)∶S(②)＝BF∶FC＝1，即S(①＋③)＝S(②)。

这就要求寻找①和③的面积比（显然直接求①号面积困难程度等同于②）。而在③＋①三角形中，再由燕尾定理，S(③)∶S(①)＝k；即S(③)＝2 S(①)，联合S(①＋③)＝S(②)可解得S(②)＝3 S(③)/2。

好了，问题解决了。回到S(②＋③＋④)＝S(□ABCD)/2＝18，把S(②)＝3 S(③)/2和S(④)＝6代入，解得S(③)＝12/5。

最后，阴影面积＝S(△BDF)－S(③)且S(△BDF)＝S(□ABCD)/4＝9（见前），解得：阴影面积＝21/5＝4.2。

另：附带可解得，GH∶HC＝S(③)∶S(②)＝2:3，以及DH∶HF＝4:1。所以，可以体会一下由面积比求得线段比，何时可以走这条路。

本文内容由小姿整理编辑！