三角形倍角模型辅助线的做法(倍角问题怎么做辅助线)

导语：中考几何压轴 13 辅助线法则 终极经典解析 倍角三角形 性质应用

中考几何压轴 13辅助线法则 终极经典解析 倍角三角形 性质应用

这一系列，不限专题，解析系列经典几何题，提高几何分析解决问题能力。

题16. 《倍角三角形性质应用》

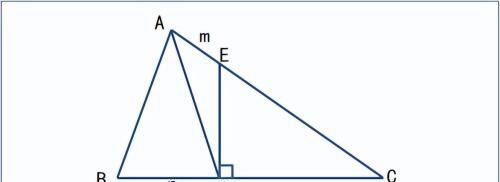
如图，AD是∠A平分线，过D作DE⊥BC，∠C＝2∠ADE，AE＝m，BD＝n，则CD＝ 。

〖一般性提点〗

如果对倍角三角形性质比较熟练，解题速度可以快一些。本题选自中考填空题，速度是重要因素。

从角度分析起步，按部就班，并不是有难度的几何题。角度分析的目的，自然是为了获得线段信息。

借机复习一下倍角三角形的三个性质，不代表本题一定用到。可参考《中考几何进阶 30 辅助线法则 倍角三角形》

倍角 三角形 性质1

倍角边与单角边和、差之积＝单角边与第三边之积。

倍角 三角形 性质2

第三角平分线分第三边为两段，其中倍角邻边＝倍角（对）边－单角（对）边。

倍角 三角形 性质3

第三边垂足与中点间线段长度＝单角边之半。

〖题目分析〗

求线段长度，一般有解Rt三角形和利用相似三角形两大基本方法。相似三角形方法当然蕴含了角平分线定理。

一般总是从角度分析起步。角度分析是不二的法门，再强调一次。

设∠A＝2α，∠ADE＝θ。

则：

[1].依题设，∠C＝2θ

[2].∠AED＝α＋θ（△ADE外角）

[3].Rt△CDE中：α＋3θ＝90°

[4].△ABC中：2α＋2θ＋∠B＝180°

[5]. [4] － [3] × 2得∠B＝4θ

至此，除了明了△ABC是倍角三角形，没有更多的直接信息。再往下就需要考虑辅助线了。

[6].辅助线

既可以根据倍角三角形性质，也可以基于角平分线的特点，过B作AD的垂线，其延长线交AC于F。则△ABF为等腰三角形，AB＝AF。FC＝BD＝n（倍角三角形性质2，不知道问题不大，参考后注）。

[7].连接DF，易知△ABD≌△AFD，∠AFD＝4θ

[8]. ∠FDC＝2θ: F是Rt△CDE斜边EC的中点：

[9]. EF＝FC＝n

[10].AB＝AF＝m＋n

[11].由角平分线定理：CD/BD＝AC/AB，解得CD＝(m＋2n)n/(m＋n)。

------

注：稍加更多的角度分析，可知DF＝BD＝n，从而FC＝EF＝DF＝n.

时间估算：[1]至[5]:＜10秒？[6]至[11]：＜15秒？呵呵。

熟练者，可跳跃直接做出BF、DF辅助线。

本文内容由小楠整理编辑！