从一道题目看出初高中衔接的重要性的作文(初高中衔接的问题)

导语：从一道题目看出初高中衔接的重要性

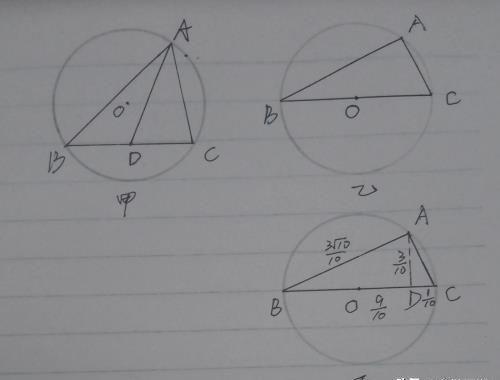
例题:O为△ABC外接圆的圆心，满足2AO＝AB+AC3，BA在BC上的投影向量为9/10BC，则Cos∠AOC的值是？（原题没有图，黑体字代表向量）

本题涉及到的知识点较多，有向量的平行四边形法则，投影向量的定义，直角三角形射影定理，圆心角与圆周角的关系，三角函数等，综合性较强。

其中直角三角形射影定理属于初高中衔接的知识，初中涉及少，老师一带而过，到了高中做题就要直接运用，如果没掌握，很有可能就解不出类似题目，所以又一个实例证明初高中衔接的重要性。其实直角射影定理的证明也很简单，利用相似三角形即可证出。但是，孩子考试时，时间紧，压力大，如果对这方面知识比较陌生，可能就不往这个方向上想。

初高中数学衔接，不是说提前学高中的知识，是要学初中没学到位，高中却要求掌握的知识。提前买一本书，不用那么贵的，十块八块就有，让孩子找时间看看。

刚接触向量，不太熟练，可以先随意画个三角形，如图甲所示，发现AB+AC应该等于2AD，D为BC的中点。而已知2AO＝AB+AC，所以AD＝AO，D点与O点重合，因此，BC为△ABC外接圆的直径，△ABC是直角三角形。∠AOC为AC对应的圆心角，大小等于其对应的圆周角的两倍，即∠AOC＝2B。Cos∠Aoc＝2Cos²B-1，求出CosB即可求出本题的解。

重新画图，如图丙所示。过A点作AD垂直BC于点D，假设BC长度为1，根据已知条件，BD＝9/10，在Rt△ABC中，AD为斜边上的高，根据直角三角形射影定理，AD²=BD·DC，求出AD＝3√10/10，得出CosB＝3√10/10，于是Cos∠Aoc＝2Cos²B-1＝2（3√10/10）²-1＝4/5。

本文内容由小姬整理编辑！