中考几何题目经典的辅助线手法(初中数学几何题辅助线的做法)

导语：中考几何进阶 辅助线法则（14）角度分析：几何题解2

中考几何进阶 辅助线法则（14）角度分析：几何题解2

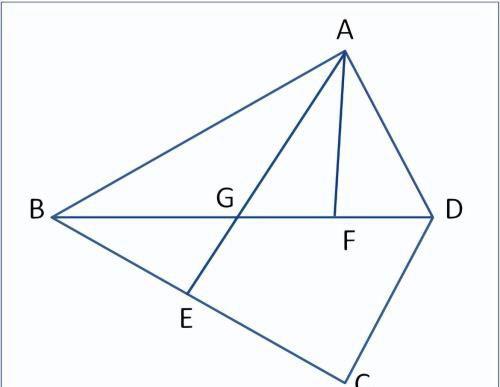
例题1 如图已知：△ABD和△CBD关于直线BD对称，点E、F分别是线段BC和线段BD上的点，且点F在线段EC的垂直平分线上，连接AF、AE，AE交BD于点G．求证：∠EAF=∠ABD.

〖分析〗

证明角度相等的几个一般思路：1）等腰三角形的底角；2）相似或全等三角形对应角；3）平行四边形对角；4）同弧（同弦）上的圆周角；5）平行线与第三条直线相交的同位角或内错角。

依据题设，考察哪条路可以走得通。

角度分析

轴对称既提供了等量线段，也给了角度相等；线段垂直平分线同样如此。

利用对称关系，∠CBD=∠ABD，求证∠EAF=∠ABD等同于求证∠EAF = ∠CBD。

题设F在线段EC的垂直平分线上，连接EF、CF以补全等腰三角形，并作底边的高FH，垂足为H，则EF＝CF，如图。

从题解图不难发现，要证明所求，只要能证明ABEF四点共圆，而这只需证明四边形ABEF对角互补，或外角等于内对角。

由题设对称关系（BD为对称轴，FH为EC垂直平分线），不难发现：

∠BAF＝∠BCF＝∠CEF＝γ，∴ABEF四点共圆。

于是，∠EAF=∠CBD＝∠ABD＝α，所求得证。

题后：1）线段垂直平分线意味着等腰三角形，无论是否有用，先补全相应的等腰三角形再看。2）根据所求，先一般性思考可能的方法手段，才是做题的真正目的。

--------

例题2 △ABC中，∠B＝90°，M为AB上一点，使得AM＝BC，N为BC上一点，使得CN＝BM。连接AN、CM交于P点。求∠APM的度数。

〖分析〗

除了∠B＝90°（垂直），都是线段相等关系，要求的是角度数。那么这个角度肯定是“特殊角”，无外乎30°、45°、60°以及它们的补角。那么思路就在于构筑特殊的三角形，无非是等边三角形，或者含特殊角的直角三角形。

本题角度的位置比较尴尬：和已知的线段相等不搭边，所以角度的位置要转移。

一般地（和具体的题无关），和前面的例题思路一样，角度转移无非通过：1）等腰三角形的底角；2）相似或全等三角形对应角；3）平行四边形对角；4）同弧（同弦）上的圆周角；5）平行线与第三条直线相交的同位角或内错角。

本题另一个思路，是题设有垂直线段，线段相等，所以三垂直模型也可以考虑。为此，先复习一下《三垂直模型》。

--------

三垂直模型

在以前辅助线法则文章中，《法则九》归纳为：三垂直，边相等，等腰直角含其中。

在三垂直前提下，

(1) AB＝AC；

(2) AP＝CQ；

(3) AQ＝BP；

(4) PQ＝PB＋QC

这四个论断中，如果有一个成立，则另外三个必定成立。

--------

1）题设有AM＝BC，AB⊥BC，考虑三垂直模型。有两种说法。

1°AD⊥AB，取AD＝BM，连接CD、DM。

2°过A作AB垂线，过M作CM垂线，相交于D，连接CD。

无论哪种都可以，见图。

易证，四边形ANCD为平行四边形，△AMD≌△CMB。然后不难证明△CMD为直角等腰三角形，最终∠APM＝45°。

2）作平行线，将∠APM转移。

无非是过A、N、C、M（构成角的线段端点）中的一点作平行线，或平行于CM，或平行于AN（AP）。

1°过C作CD∥AP，交过A点的垂直于AB的直线于D，题解图等同于三垂直题解图。

2°过A作CM的平行线，与过C作AM的平行线交于D点，连接DN。见图。

不难证明△AND为等腰直角三角形：α＋β＝90°☞ CM⊥DN ☞ AD⊥DN（∵AD∥CM），DN＝CM＝AD。

3°过M作AN的平行线，同时过N作AM的平行线，二者相交于D，连接CD。见图。

△DNC≌△CBM ☞ α＋β＝90°☞ ∠MCD＝90°且CM＝CD ☞ △MCD为等腰直角三角形：∠APM＝∠CMD＝45°。

4°过N作CM的平行线，过M作CN的平行线，二者相交于D。连接AD，见图。

△AMD△CBM ☞ α＋β＝90°☞ ∠ADN＝90°且AD＝CM＝ND，☞ △AND为等腰直角三角形：∠APM＝∠AND＝45°。

本文内容由小若整理编辑！