解题方法和技巧(解题方法大全)

导语：解题的方法与技巧（四）

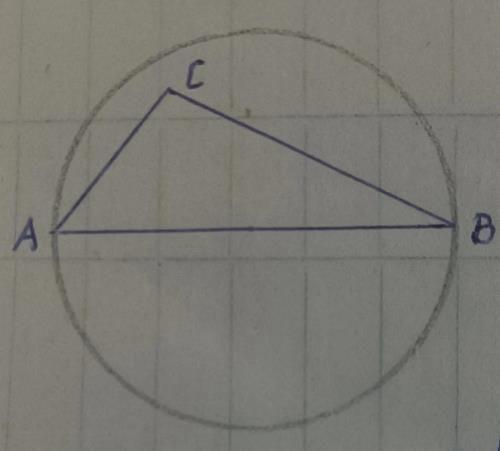
6.平面上给定100个点，已知其中任意两点的距离不超过1，且任意三点所成的三角形是钝角三角形。证明：这100个点被一个半径为1/2的圆覆盖。

证明：设这100个点中，以A,B两点间的距离最大。我们以线段AB为直径作一个圆，由于AB<=1,所以此圆的半径<=1/2.

现在其余的98个点中任取一点C,因为AB>=AC,AB>=BC,又由题设可知△ABC是钝角三角形，所以角C一定是钝角，即C点位于以AB为直径的圆内，也就是说这100个点都被这个圆所覆盖。

7.平面上有n个点，其中任意三点作成的三角形的面积都小于1.试证存在一个面积小于4的三角形包含这n个点。

证明：这n个点可作成的三角形的数目是有限的（为Cn-3个），其中必有面积最大的一个(若面积最大的三角形不止一个，则任取一个)，设为△A1A2A3,过顶点A1,A2,A3分别作对边的平行线，得到一个△ABC,显然，

S△ABC=4S△A1A2A3<4.

若△ABC外还有这n个点中的一点，设为A4,于是有S△A4A3A1>S△A2A3A1.

这与△A1A2A3的面积最大矛盾。于是△A1A2A3即为所求。

8.空间中给出了8个点，其中任意4个点都不在同一平面上，在它们之间连以17条线段。证明：这些线段至少形成了一个三角形。

证明：首先设连出线段数目最多的点为A,且设它共连出n条线段。如果所有17条线段都没有形成三角形，那么与A相连的n个点之间彼此都没有线段相连。而其余的7-n个点中，每一个点所连出的线段条数不多于n条。因此，线段的总数目不超过

n+(7-n)n=n(8-n)<=[(n+8-n)/2]^2=16.

这与已知的有17条线段相矛盾。从而此命题成立。

本文内容由小薇整理编辑！